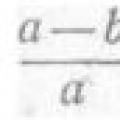頻繁 幾何学的な力ベクトルの追加には必要があります 複雑で面倒な建設物。 そのような場合に彼らが頼るのは、 別の人に方法、幾何学的構造 交換された計算について スカラー量 これは達成されました 指定された力を直交座標系の軸に投影することによって。
数学からよく知られているように、 軸呼ばれた 無限の直線、それに特定の 方向. ベクトルの軸への投影は スカラー決められた値 軸セグメント、 切り落とす 垂線、 省略 ベクトルの最初と最後から軸に。
ベクトルの投影を考慮します ポジティブ (+ )、方向が投影の開始から終了までの場合 マッチ正の軸方向です。 ベクトルの投影を考慮します ネガティブ (- )、方向が投影の開始から終了までの場合 反対軸の正方向。
シリーズを検討してみよう 軸上の力を設計する場合.
- パワーを考えると R （米。 あ )、軸と同じ平面上にあります。 バツ 。 力ベクトルは軸の正の方向と鋭角を形成します α .
値を見つけるには 投影、力ベクトルの最初と最後から、軸に対する垂直線を下げます。 バツ、 我々が得る
Р x = ab = Р cos α .
この場合のベクトルの射影 ポジティブ.
2. 与えられた力 Q （米。 b )、軸と同じ平面上にあります。 バツ 、ただし、そのベクトルは軸の正の方向と鈍角を作ります。 α .
力の投影 Q 軸ごと バツ
Q x = ab = Q cos α、
ということで = - cos β .
なぜなら α > 90° 、その後、cos コス α - ネガティブサイズ。 表現した上で コス α を通して cosβ (β - 鋭角)、最終的に得られるのは
Q x = - Q cos β
この場合、力の投影は、 ネガティブ.
それで、 軸への力の投影 座標は次と等しい 力の大きさと、力ベクトルと軸の正の方向との間の角度の余弦との積.
力ベクトルの軸への投影を決定するとき、通常はコサインが使用されます。 急性正または負のどの軸方向に形成されるかに関係なく、角度が変化します。 サイン突起を直接取り付ける方が簡単です 図面によると。
平面上にある力 xOy 、2 つの座標軸に投影できます。 おお そして OU 。 図面を見てみましょう。
強さを見せてくれる R とその予測 処方箋 そして RU 。 突起同士が形成されるため、 真っ直ぐ直角三角形からの角度 ABC 以下に続きます:
次に、静力学の問題を解決するための解析的 (数値的) 手法について考えてみましょう。 この方法は、軸への力の投影の概念に基づいています。 他のベクトルと同様に、軸への力の投影は、力の始まりと終わりの投影の間に囲まれた、適切な符号が付いたセグメントの長さに等しいスカラー量です。 投影には、その開始から終了までの動きが軸の正の方向に発生する場合にはプラス符号が付き、負の方向に発生する場合にはマイナス符号が付きます。 この定義から、任意の平行かつ同一方向の軸上への所与の力の射影は互いに等しいことがわかります。 これは、力と同じ平面上にない軸への力の投影を計算するときに使用すると便利です。
米。 1
軸上への力の投影を示します おお象徴になろう Fバツ。 次に、図 1 に示されている力について、次の式が得られます。
しかし、図面から明らかなように、
したがって、
つまり、軸への力の投影は、力の係数と、力の方向と軸の正の方向との間の角度の余弦との積に等しくなります。 この場合、力の方向と軸の正の方向の間の角度が鋭角であれば投影は正となり、この角度が鈍角であれば負になります。 力が軸に垂直な場合、軸への投影はゼロになります。
図2
平面上への力の投影 おおおおは、力の始まりと終わりをこの平面に投影したものの間に囲まれたベクトルと呼ばれます (図 2)。 したがって、軸上への力の投影とは対照的に、平面上への力の投影は、数値だけでなく平面内の方向によっても特徴付けられるため、ベクトル量です。 おおおお。 モジュロ。ここで、 は力の方向とその投影の間の角度です。
場合によっては、軸上への力の投影を見つけるには、最初にこの軸が存在する平面上への投影を見つけてから、平面上で見つかった投影をこの軸上に投影する方が便利な場合があります。
たとえば、図のような場合です。 2、次のような方法で見つけます。
力を加える幾何学的な方法。
力学における多くの問題の解決は、ベクトル代数で知られるベクトル、特に力の加算操作に関連しています。 任意のシステムの力の幾何学的和に等しい量は、この力のシステムの主ベクトルと呼ばれます。 力の幾何学和の概念を合力の概念と混同しないでください。後で説明するように、多くの力の系では合力はまったく存在しませんが、幾何学和 (主ベクトル) は計算できます。あらゆる力の体系に。
力の系の幾何学和 (主ベクトル) は、平行四辺形の法則に従った系の力の逐次加算によって、または力の多角形の構築によって決定されます。 2 番目の方法はより簡単で便利です。 この方法を使用して力の合計を求めるには (図 3、 ある）、任意の点を除いて について(図3、 b) ベクトル オア、選択したスケールで力を表します F 1、ポイントから ある力を表すベクトルを脇に置きます F 2、ポイントから bベクトルを脇に置く 紀元前、強さを表現 F 3など。 端から メートル最後から二番目のベクトル ん、強さを表現 F n.最初のベクトルの先頭と最後のベクトルの末尾を接続すると、ベクトルが得られます。 , 追加される力の幾何学的合計または主ベクトルを表します。
大きさと方向は、力ベクトルがプロットされる順序には依存しません。 行われた構築は、べき乗の三角形ルールを一貫して適用した結果であることが簡単にわかります。
図3
図で構築された図。 3、 b、と呼ばれる (一般的な場合はベクトル) ポリゴンを強制します。 したがって、いくつかの力の幾何学的合計または主ベクトルは、これらの力から構築された力多角形の後側によって表されます (力多角形ルール)。 ベクター ポリゴンを作成するときは、ベクトルのすべての項の矢印が一方向 (ポリゴンの輪郭に沿って) を向く必要があり、ベクトルの項は反対方向を向く必要があることに注意してください。
力が集まった結果。静力学を研究するときは、より単純な力の系からより複雑な力の系へ順次移行していきます。 まず、力が集まるシステムを考えてみましょう。
収束する作用線がシステムの中心と呼ばれる一点で交差する力は力と呼ばれます (図 3 を参照)。 あ).
静力学の最初の 2 つの公理の結果、絶対剛体に作用する収束力系は、1 点に加えられる力系と等価になります (図 3、 あ時点で あ).
力の平行四辺形の公理を一貫して適用すると、収束する力の系の結果はこれらの力の幾何学和 (主ベクトル) に等しく、それらの交点に適用されるという結論に達します。 したがって、力が点に集中すると、 あ(図3、 あ)、力の多角形を構築することで検出され、その点に適用される主ベクトルに等しい力 あ、この力のシステムの結果になります。
ノート
1. 合力のグラフィック決定の結果は、力が異なる順序で合計されても変わりませんが、この場合、最初のものとは異なる、異なる力の多角形が得られます。
2. 実際、特定のシステムの力ベクトルで構成される力の多角形は破線であり、通常の意味での多角形ではありません。
3. 一般の場合、この多角形は空間図形であるため、合力を決定するためのグラフィカルな方法は力の平面系にのみ便利であることに注意してください。
力が収束するシステムの平衡。
力学の法則から、相互にバランスの取れた外力によって作用される剛体は、静止しているだけでなく、運動することもできることがわかります。これを「慣性による」運動と呼びます。 このような動きは、たとえば、物体の前方への均一な直線運動などです。
ここから、2 つの重要な結論が得られます。
1) 静的平衡の条件は、静止している物体と「慣性によって」移動している物体の両方に作用する力によって満たされます。
2) 自由固体物体に加えられる力のバランスは、物体自体の平衡 (静止) にとって必要な条件ではありますが、十分な条件ではありません。 物体は、それが静止していた場合にのみ、そしてそれに平衡した力が加えられる瞬間まで、静止したままになります。
固体に加えられる収束力の系が平衡するためには、これらの力の合力がゼロに等しくなることが必要かつ十分です。 力自体が満たさなければならない条件は、幾何学的形式または分析形式で表現できます。
1. 幾何学的平衡状態。 収束する力の合力は、これらの力から構築された力多角形の閉じる側として定義されるため、多角形内の最後の力の終わりが最初の力の始まりと一致する場合に限り、消滅する可能性があります。 つまり、ポリゴンが閉じたときです。
したがって、システムが平衡状態にあるためには、収束する力が必要かつ十分であり、これらの力から構築される力の多角形が閉じられます。
2. 分析平衡条件。 解析的には、収束力系の合力は次の式で求められます。
.
ルートには正の項の合計が含まれているため、 Rがゼロになるのは、同時に の場合、つまり物体に作用する力が以下の等式を満たす場合のみです。
等式表現 分析形式の平衡条件: 力が収束する空間システムの平衡のためには、3 つの座標軸のそれぞれに対するこれらの力の投影の合計がゼロに等しくなることが必要かつ十分です。
物体に作用するすべての収束力が同じ平面内にある場合、それらは収束力の平坦なシステムを形成します。 力が収束する平らなシステムの場合、明らかに 2 つの平衡条件しか得られません。
等式は、収束する力の作用下での自由剛体の平衡に必要な条件 (または方程式) も表します。
三力定理。 3 つの非平行な力の平衡平面システムは収束します。
定理の定式化において「フラット」条件は必要ありません。3 つの力のバランスがとれたシステムは常にフラットであると確信できます。 これは、任意の空間力系の平衡状態から得られますが、これについては後で説明します。
例1.図 4 は 3 つの力を示しています。 軸上の力の投影 x、y、z明らかです:
図4
|
まず力を平面に投影します バツについて で、軸が配置されている場所 (図 4)、大きさのベクトルを取得し、それを軸に投影します。 バツ： .
同様に進めて、軸への投影を見つけます。 で: .
軸への投影 zより簡単に見つかります: 。
軸上の力の投影を確認するのは簡単です。 Vは同じ：
これらの投影を決定するときは、力と軸の位置を上から見た図である図 5 を使用すると便利です。
図5
力の収束系(図6)に戻りましょう。 力の作用線の交点を原点とした座標軸を描きましょう。 について.
力の合力であることはすでにわかっています。 このベクトルの等価性を軸に投影してみましょう。 軸上の結果の投影を取得します バツ, y, z:
それらは、対応する軸上への力の射影の代数和に等しい。 そして、結果の射影がわかれば、その値を直方体の対角として決定できます。 
または
方向余弦を使用してベクトルの方向を求めます (図 6)。
図6
例2。重さのあるボールに R、水平面に横たわり、糸で縛られている AB、力が働きます F(図7)。 結合の反応を定義しましょう。
図7
すべての静的問題は、同じスキームに従って特定の順序で解決されることにすぐに注意してください。
この問題を解決する例を使用してそれを示してみましょう。
1. 平衡の対象、つまり未知のものを見つけるためにその平衡を考慮すべき物体を選択する (割り当てる) 必要があります。
この問題では、もちろん、平衡の対象はボールです。
2. 設計図の作成。 計算スキームは平衡の対象であり、接続のない自由体として個別に描かれており、反力やその他の力が作用します。
糸の反応と平面の通常の反応を示します (図 7)。 それらに加えて、与えられた力がボールに作用します。
3. どのような力系が得られるかを確立し、対応する平衡方程式を作成する必要があります。
ここでは、平面内に配置された収束力の系があり、それに対して 2 つの方程式を作成します (軸は任意に描くことができます)。
4. 連立方程式を解き、未知数を見つけます。
問題の状況に応じて、平面上のボールの圧力を見つける必要があります。 そして、ボールに対する飛行機の反応を発見しました。 しかし、定義により、これらの力は大きさが等しく、平面にかかる圧力だけが反対方向、つまり下方向に向けられることになります。
例 3.体重 R 3 本のロッドによって垂直面に取り付けられています (図 8)。 ロッドにかかる力を求めてみましょう。
図8
この問題では、平衡の対象となるのはノードです。 と荷物と一緒に。 それは、反力、ロッドにかかる力、重量と別々に描画されます。 力は、力が収束する空間システムを形成します。 3 つの平衡方程式を作成します。
最初の方程式から次のようになります。 S 2 =S 3. 続いて3つ目からは、
そして2番目からは、
ノードから、つまり平衡の対象からロッドに力を向けたとき、ロッドは張力で働いていると仮定しました。 ロッドフォース CD陰性であることが判明した。 これはロッドが圧縮されていることを意味します。 したがって、ロッドにかかる力の符号は、ロッドがどのように機能するか、つまり引張または圧縮の状態を示します。
例4.ヒンジで接続されたロッドの反応を決定する で、荷物の重さを量る場合 Q(図9、 あ).
解決。上記で提案された計画に従って、均衡を考慮する団体を選択します。 この選択は主に問題の条件によって決まります。 この問題で吊り荷の平衡を考慮すると、物体の重量に等しい糸の張力のみを求めることができます。 T = Q(図9、 b).
ロッドの反応を決定するには、平衡点を考慮します。 で。 ねじ山を介してアクティブな力が加えられていると仮定できます。 Q拒否されたロッドの反応 S Aそして S C(図9、 V).
この問題を分析的に解決してみましょう。 点での原点の選択 で、次の形式の平衡方程式を作成しましょう。
-S A cosα+ S C cosβ = 0;
S Aシンα+ S C sinβ = Q.
ここから探すには S C結果として得られる方程式を加算してみましょう。最初に最初の方程式に sinα を乗算し、2 番目の方程式に cosα を乗算します。
S C(sinαcosβ + cosα sinβ) = Qコスα。
したがって、 S C = Q cosα/sin(α+β)、α と β はこれらの方程式に対称的に入るので、 S A = Q cosβ/sin(α+β)。
問題の分析解の正しさをチェックするために、グラフィック手法を使用します。
3 つの力から形成される三角形: Q,S Aそして S Cは閉じている必要があるため、解決策は既知の辺に沿って三角形を構築することになります ( Q) と他の 2 つの辺の方向( S Aそして S C）。 これを行うには、スケーリングするベクトルを構築する必要があります Qそして、このベクトルの最初と最後から平行な直線を引きます。 S Aそして S C交差点の手前（図9、 G).
見つかったセグメントの長さを測定し、縮尺に合わせて再計算したら、問題は解決したと考えることができます。 結果として得られるベクトルの方向は、力のポリゴンが閉じているという条件から決定されます。つまり、最後のベクトルの終わりが最初のベクトルの始まりと一致する必要があります。
図9
ただし、値を決定することは可能です S Aそして S Cスケール バーを使用せず、構築された三角形を単純に解く場合。
この目的のために、サイン定理を使用します。
したがって、補角のサインをコサインに置き換えると、次のようになります。
つまり、グラフィック解の結果が解析結果と一致しており、問題が正しく解決されたことを意味します。
例5。無重力の理想的なブロックの中心は、点でヒンジでつながれた 2 本のロッドによって保持されています。 で。 一端が固定されたブロックに糸を通し、荷重を計ります。 Q(図10、 あ). ブロックの寸法を無視して、ロッドの反応を決定します。
解決。ブロックの均衡を考慮する で、糸の張力が適用される T 1と T 2 廃棄ロッドの反応と S Aそして S C、前の例と同様に、引き伸ばされたものとみなします (図 10、 b).
実際には、負荷の重量が有効力として作用します。 Q、スレッドを使用してブロックに取り付けられているため、 T 1 = Q。 強度について T 2 理想的な、つまり摩擦のないブロックは、糸の張力の方向を変える機構ですが、その大きさではないことに注意してください。 T 1 = T 2 = Q.
ブロックの寸法を無視すると、その点に適用される収束力のバランスのとれたシステムが得られます。 で(図10、 V).
反応を定義しましょう S Aそして S C分析的に。 解析平衡方程式の最初の式に両方の未知数が含まれる場合、方程式 Σ やあ= 0 未知の反応 S Cは含まれないため、次の方程式を使用して問題を解き始めるのが合理的です。
S A cos30°+ T 2 cos60°- T 1 = 0.
ここに三角関数の値を代入すると、 T 1 = T 2 = Q、 我々が得る：
さて、方程式Σに戻りましょう。 Xi = 0:
- S A cos60°+ T 2 cos30°+ S C= 0,
上記の値を代入します S A、 我々が得る：
この場合、最後の式のマイナスはロッドが 太陽予想したように伸ばされておらず、圧縮されています。
得られた結果を確認するために、この問題をグラフィカルに解いてみましょう。 そのために、センターからは について既知の力を一貫してスケールでプロットします T 1と T 2、最初のベクトルの始まりと最後のベクトルの終わりから平行な直線を描きます。 S Aそして S C交差点の手前（図10、 G).
図10
構築された力の多角形には対称軸があり、| があることが簡単にわかります。 S A|=|S C|。 この場合、ベクトルの方向は、 S C図面に示されている元の方向とは反対の力のポリゴン、つまりロッド上で 太陽伸ばされるのではなく、圧縮されます。
ノート
1. 解析平衡方程式系では、座標軸は相互に垂直である必要はありません。したがって、最後の例で軸を選択した場合、 おお、力の方向と一致します。 T 2、未知数を求める方程式系が得られます。 S Aそして S Cは 互いに独立して.
2. 続いて、分析ソリューションがグラフィック ソリューションを使用するだけでなく、分析的にも検証できることがわかります。 ただし、力が収束するシステムの場合、問題を解決するための前述の方法が明らかに最適です。
フォース ポリゴンの構築には複雑で面倒な構築が必要であり、十分に正確な結果が得られません。 そのような場合、彼らは幾何学的な構築をスカラー量の計算に置き換える別の方法に頼ります。 これは、指定された力を直交座標系の軸に投影することによって実現されます。
軸とは、特定の方向が割り当てられた直線です。ベクトルの軸への射影はスカラー量であり、ベクトルの始点と終点から垂線を垂らして軸を切り取った部分によって決まります。
投影の開始から終了までの方向が軸の正の方向と一致する場合、ベクトル投影は正 (+) とみなされます。 投影の開始から終了までの方向が軸の正の方向と反対の場合、ベクトル投影は負 (-) とみなされます。
軸に力を投影するいくつかのケースを考えてみましょう。
1. 力を与える（図7、 あ)、軸と同じ平面上にあります。 バツ。 力ベクトルは軸の正の方向と鋭角 α を形成します。 投影の大きさを見つけるには、力ベクトルの最初と最後から軸に垂直な線を下げます。 バツ; 我々が得る
P x = ab = P cos α. (4)
この場合のベクトルの射影は正です。
2. 力を与える（図7、 b)、軸と同じ平面上にあります。 バツ、ただし、そのベクトルは軸の正の方向と鈍角 α を作ります。 力の投影 Q軸ごと バツネガティブ
Q x = - ab = - Q cos α。 (5)
3. 与えられた力 、軸に垂直 バツ(図7、c)。 力の投影 軸ごと バツはゼロに等しい、つまり N x = N cos 90° = 0.
それで、 座標軸上への力の投影は、力の係数と、力ベクトルと軸の正の方向との間の角度の余弦との積に等しい。.
平面上にある力 xOy(図 8)、2 つの座標軸に投影できます 牛そして オイ。 図は力とその投影を示しています ピクセルそして パイ。 突起同士が直角をなすため、直角三角形から ABC以下に続きます:
(6)
これらの公式は、座標軸への投影がわかっている場合に、力の大きさと方向を決定するために使用できます。
理論資料
繋がり力の影響下で他の物体の動きを妨げる物体です。
コミュニケーション反応- 接続自体の内部で生じる力。 反応は常に、接続が体の動きを妨げる方向とは逆になります。 すべての身体は自由である場合もあれば、自由でない場合もあります。 自由な身体には何のつながりもありません。 自由でない物体は、その物体に作用する結合が反応によって置き換えられる場合、自由なものとして表現できます。
接続の種類:
A) 滑らかな表面または平面つまり、摩擦のない表面です。 この接続の反作用は常に接触点に対して垂直に向けられます。 R – 結合反応
b) スムーズなサポートこの接続の反応は、接触点に対して垂直に方向付けられます。 (反力は構造内の力です)。 その大きさは材質、大きさ、外力によって異なります。
V) 柔軟なコミュニケーション- ケーブル、ロープ、またはチェーンによって実行される、張力下でのみ機能する接続。 フレキシブル接続部の反力は、接続部自体に沿って固定点に向けて、つまり力の方向と反対方向に向けられます。
G) 剛性ロッド。 これは、さまざまなビーム、I ビーム、チャネルによって実行されます。 接続は引張と圧縮の両方で機能します。 ロッドが張力を受けている場合、反力はロッドに沿って固定場所に向けられ、ロッドが圧縮されている場合、反力はロッドの後方に向けられます。
d) 多関節サポート。 サポートは可動式または固定式にすることができます。 固定支持体には、互いに垂直に配置された 2 つの反応があります。 可動サポートには、表面に対して垂直な 1 つの反力があります。
可動サポート 固定サポート
作業を完了するためのタスク
1. あなたのバージョンの絵を描きます。
2. 図面について説明します。
3. 接続のタイプを決定し、それらをリアクションに置き換えます。
オプション 18
1.
 | 2.
 | 3.
|
コントロールの質問:
1. 軸と投影の違いは何ですか?
2. 問題を解くときに、いくつの平衡方程式を作成しましたか?
3. PSSS 問題を解決するための方法論。
4. 収束する力の平面系を定義します。
5. 座標面への力の投影の大きさはどれくらいですか?
文学：
1. ベレイン L.I. 技術力学 - M: アカデミー、2006 年。
2. モヴニン M.S. 技術力学の基礎 - サンクトペテルブルク: 工科大学、2003 年。
3. モルチャノバ E.V.、シュリギナ G.N. 材料の静電気と抵抗 - トムスク、2008 年。
実践その２
レッスンのトピック:収束力の平面系の結合反応の決定。
レッスンタイプ:得た知識の定着。
レッスンの目的:収束力の平面系の結合反応を決定する方法を学びます
サポートとは次のことを意味します。
1. 作業を実行するための方法論的なガイダンス。
2.個別のタスク。
実務用のノート、４．
7. 電卓。
作業技術:
1. ガイドラインと提案された理論資料を注意深く検討してください。
2.オプションに従って、以下に示す方法に従ってタスクを完了します。
3.完了した作業について結論を出します。
4.セキュリティの質問に答えます。
理論資料
任意に配置された力の平面系の条件と平衡方程式。
力の系が点に到達すると、R ch と M ch が得られます。
力の系が平衡状態にある場合、R gl = 0、M gl = 0 となります。
この系の 3 種類の平衡方程式を書き留めてみましょう。
ファーストビュー
軸への力の投影は、切り取られた軸のセグメントによって決まります。
ベクトルの始点と終点から軸に下ろした垂線 (図 3.1)。
軸上の力の投影の大きさは、力の係数と力のベクトルとの間の角度の余弦の積に等しい。 正の方向軸。 したがって、投影には次の符号があります。 同じ方向に正力のベクトルと軸と ネガティブ監督するとき マイナス軸に向かって(図3.2)。
互いに直交する 2 つの軸上に力を投影(図3.3)。
仕事の終わり -
このトピックは次のセクションに属します。
理論力学
理論力学.. 講義.. トピック: 静力学の基本概念と公理..
このトピックに関する追加の資料が必要な場合、または探している資料が見つからなかった場合は、作品データベースの検索を使用することをお勧めします。
受け取った資料をどうするか:
この資料が役に立った場合は、ソーシャル ネットワーク上の自分のページに保存できます。
| つぶやき |
このセクションのすべてのトピック:
理論力学の問題
理論力学は、固体材料の機械的運動とそれらの相互作用の科学です。 機械的な運動は、空間と時間における物体の動きとして理解されます。
第三公理
物体の機械的状態を乱すことなく、バランスのとれた力のシステムを追加または削除することができます (ゼロに等しい力のシステムを破棄する原理) (図 1.3)。 P,=P2 P,=P.
第 2 および第 3 の公理の帰結
固体に作用する力は、その作用線に沿って動かすことができます (図 1.6)。
接続と接続の反応
静力学のすべての法則と定理は、自由剛体に対して有効です。 すべての身体は自由なものと束縛されたものに分けられます。 自由物体とは、動きが制限されていない物体です。
ハードロッド
図では、ロッドは太い実線で示されています (図 1.9)。 ロッドはできる
固定ヒンジ
接続点は移動できません。 ロッドはヒンジ軸の周りを自由に回転できます。 このようなサポートの反力はヒンジ軸を通過しますが、
力が集まる平面系
作用線が一点で交差する力の系を収束といいます (図 2.1)。
力が集中した結果
2 つの交差する力の合力は、力の平行四辺形または三角形を使用して決定できます (第 4 公理) (対 2.2)。
力が収束する平面系の平衡条件
力の系が平衡状態にあるとき、合力はゼロに等しくなければなりません。したがって、幾何学的構造では、最後のベクトルの終わりが最初のベクトルの始まりと一致する必要があります。 もし
幾何学的手法を使用して平衡問題を解く
システム内に 3 つの力が存在する場合、幾何学的な方法を使用すると便利です。 平衡問題を解くときは、物体が完全に固体である (固体である) と考えてください。 問題解決の手順:
解決
1. 締結ロッドに生じる力は、ロッドが荷重を支える力と大きさが等しい (静力学の第 5 公理) (図 2.5a)。 私たちは、次のような理由により考えられる反応の方向を決定します。
分析的な方法での強さ
合力の大きさは、力の系のベクトルのベクトル (幾何学的) 和に等しくなります。 結果を幾何学的に決定します。 座標系を選択し、すべてのタスクの予測を決定しましょう
分析形式で力を集中させる
結果がゼロであるという事実に基づいて、次の条件が得られます。
偶力、偶力のモーメント
力のペアは、大きさが等しく、平行で、異なる方向に向けられた 2 つの力からなるシステムです。 ペアを形成する力の系 (P; B") を考えてみましょう。
点に関する力のモーメント
物体の取り付け点を通らない力は、その点に対する物体の回転を引き起こすため、そのような力が物体に与える影響はモーメントとして推定されます。 力のモーメント相対。
力の平行伝達に関するポアンソの定理
力はその作用線に平行に伝達できます。この場合、力の係数と力が伝達される距離の積に等しいモーメントを持つ一対の力を追加する必要があります。
分散された力
任意の力のシステムの作用線は一点で交差しないため、身体の状態を評価するには、そのようなシステムを単純化する必要があります。 これを行うには、システムのすべての力が任意に 1 つに変換されます。
基準点の影響
基準点は任意に選択されます。 基準点の位置が変化しても、主ベクトルの値は変化しません。 減速点を移動する際のメインモーメントの大きさが変化しますので、
フラットフォースシステム
1. 平衡状態では、システムの主ベクトルはゼロです。 主ベクトルを分析的に決定すると、次の結論が得られます。
負荷の種類
適用方法に応じて、負荷は集中と分散に分けられます。 実際の荷重伝達が無視できるほど小さな領域 (点) で発生する場合、その荷重は集中と呼ばれます。
軸を中心とした力のモーメント
軸に対する力のモーメントは、軸と平面の交点を基準として、軸に垂直な平面に力を投影したモーメントに等しくなります (図 7.1 a)。 ムー
空間内のベクトル
空間では、力ベクトルは 3 つの相互に垂直な座標軸に投影されます。 ベクトルの投影は直方体の辺を形成し、力のベクトルは対角線と一致します (図 7.2)
空間収束力系
空間収束力系は、同じ平面内になく、作用線が 1 点で交差する力の系です。 空間システムの結果
任意の空間力系を中心 O に持ってくる
力の空間系が与えられます (図 7.5a)。 それを中心 O に持っていきましょう。力は平行して動かされる必要があり、力のペアのシステムが形成されます。 これらの各ペアのモーメントは等しい
均質な扁平体の重心
(平面図形) さまざまな平面物体や複雑な形状の幾何学的な平面図形の重心を決定する必要があることがよくあります。 平坦なボディの場合、次のように書くことができます: V =
平面図形の重心座標を求める
注記。 対称な図形の重心は対称軸上にあります。 ロッドの重心は高さの真ん中にあります。 単純な幾何学図形の重心の位置は、
点の運動学
空間、時間、軌道、経路、速度、加速度について理解し、点の動き (自然な動きと座標) を指定する方法を理解します。 指定を知る
走行距離
経路は、進行方向の軌道に沿って測定されます。 指定 - S、測定単位 - メートル。 点の運動方程式: 定義する方程式
移動速度
現在、軌道に沿った移動の速度と方向を特徴付けるベクトル量は、速度と呼ばれます。 速度は、あらゆる瞬間に向けられるベクトルです。
点加速度
大きさと方向における速度の変化率を特徴付けるベクトル量は、点の加速度と呼ばれます。 地点M1から移動する際の地点の速度
均一な動き
等速運動とは、一定の速度での運動です: v = const。 直線等速運動の場合 (図 10.1a)
等しく交互の動き
等しく変化する運動とは、接線加速度が一定の運動です: at = const。 等速直線運動用
前進
並進運動とは、移動中の物体の直線が初期位置と平行に保たれる剛体の動きです (図 11.1、11.2)。 で
回転運動
回転運動中、体のすべての点は、共通の固定軸の周りに円を描きます。 体のすべての点が回転する固定軸を回転軸と呼びます。
回転運動の特殊なケース
等速回転（角速度一定）： ω =const この場合の等速回転の方程式（法則）は次のような形になります。
回転体の各点の速度と加速度
物体は点 O を中心に回転します。回転軸から距離 RA に位置する点 A の運動パラメータを決定しましょう (図 11.6、11.7)。 パス
解決
1. セクション 1 - 不均一な加速運動、ω = φ’; ε = ω’ 2. セクション 2 - 速度は一定です - 動きは均一です。 ω = 定数 3。
基本的な定義
複雑な動きは、いくつかの単純な動きに分解できる動きです。 単純な動きは並進運動と回転運動であると考えられます。 点の複雑な動きを考える
剛体の面平行運動
平行平面、または平面とは、物体のすべての点が、検討中の基準系内の固定点に対して平行に移動する剛体の動きです。
並進および回転
面平行運動は、特定の極に対する並進運動と、この極に対する回転運動の 2 つに分解されます。 分解は決定に使用されます
スピードセンター
身体上の任意の点の速度は、瞬間的な速度中心を使用して決定できます。 この場合、複雑な動きは、異なる中心を中心とした回転の連鎖として表現されます。 タスク
力学の公理
力学の法則は、数多くの実験や観察の結果を一般化したものです。 通常公理とみなされている力学の法則はニュートンによって定式化されましたが、第 1 法則と第 4 法則もまた、
摩擦の概念。 摩擦の種類
摩擦は、1 つの粗い物体が別の粗い物体の表面上を移動するときに発生する抵抗です。 物体が滑るときには滑り摩擦が発生し、転がるときには転がり摩擦が発生します。 自然サポート
転がり摩擦
転がり抵抗は土壌とホイールの相互変形に関連しており、滑り摩擦よりも大幅に小さくなります。 通常、土壌はホイールよりも柔らかいと考えられており、その場合、土壌は主に変形し、
無料ポイントと無料以外のポイント
空間内の移動が接続によって制限されない物質点は、自由と呼ばれます。 問題は力学の基本法則を使用して解決されます。 それでは材料
慣性力
慣性とは、自分の状態を変化させずに維持する能力であり、これはすべての物質体の内部特性です。 慣性力とは、物体の加速時や制動時に発生する力です。
解決
有効な力: 駆動力、摩擦力、重力。 支持体Rの反力。加速度と逆方向の慣性力を加えます。 ダランベールの原理によると、プラットフォームに作用する力のシステム
合力によって行われる仕事
力系の作用下で、質量 m の点は位置 M1 から位置 M2 に移動します (図 15.7)。 力の系の影響下で移動する場合は、次を使用します。
力
仕事のパフォーマンスと速度を特徴付けるために、パワーの概念が導入されました。 電力 - 単位時間当たりに実行される仕事量:
回転力
米。 16.2 物体は点 M1 から点 M2 まで半径の円弧に沿って移動します M1M2 = φr 力の仕事
効率
それぞれの機械や機構は、作業を行う際に、有害な抵抗を克服するためにエネルギーの一部を費やします。 したがって、機械（機構）は、有用な作業に加えて、追加の作業も実行します。
運動量変化定理
質点の運動量は、その点の質量と速度 mv の積に等しいベクトル量です。 運動量のベクトルは一致します
運動エネルギーの変化に関する定理
エネルギーとは、身体が機械的仕事を行う能力です。 機械エネルギーには、位置エネルギーまたは位置エネルギーと運動エネルギーの 2 つの形式があります。
物質点系の力学の基礎
相互作用力によって接続された一連の物質点を機械システムと呼びます。 力学におけるあらゆる物質体は機械とみなされます
回転体の力学の基本方程式
外力の作用下で剛体が角速度でオズ軸の周りを回転するとします。
電圧
断面法では、断面内の内力係数の値を決定できますが、断面全体にわたる内力の分布の法則を確立することはできません。 n の強さを評価するには
内力要因、張力。 図の構築
断面における長手方向の力と垂直応力について理解します。 縦力と垂直応力の図を作成するためのルール、分布法則を理解する
縦方向の力
軸に沿って外力が負荷された梁を考えてみましょう。 梁は壁に固定されています（締結「固定」）（図20.2a）。 ビームを積載エリアに分割します。 ローディングエリア付き
平坦部の幾何学的特徴
軸方向、遠心方向、極慣性モーメント、主中心軸、主中心慣性モーメントを決定するための物理的意味と手順について理解します。
断面積の静モーメント
任意のセクションを考えてみましょう (図 25.1)。 断面を微小な領域 dA に分割し、各領域に座標軸までの距離を乗じて積分すると、
遠心慣性モーメント
断面の遠心慣性モーメントは、両方の座標にわたる基本面積の積の合計です。
アキシアル慣性モーメント
同じ平面内にある特定のヤードに対するセクションの軸方向の慣性モーメントは、領域全体にわたる基本領域の距離の 2 乗による積の和と呼ばれます。
断面の極慣性モーメント
特定の点 (極) を基準とした断面の極慣性モーメントは、領域全体にわたる基本領域とその点までの距離の 2 乗の積の合計です。
最も単純なセクションの慣性モーメント
長方形の軸方向慣性モーメント (図 25.2) 直接想像してください
円の極慣性モーメント
円の場合、まず極慣性モーメントを計算し、次に軸方向の慣性モーメントを計算します。 無限に薄いリングの集合として円を想像してみましょう (図 25.3)。
ねじりひずみ
円形ビームのねじれは、長手方向軸に垂直な面内のモーメントを伴う力のペアが負荷されるときに発生します。 この場合、ビームの母線は角度 γ だけ曲げられ、回転します。
ねじれに関する仮説
1. 平坦な断面の仮説は成り立ちます。梁の断面は平坦で長手方向の軸に垂直で、変形後も平坦で長手方向の軸に垂直なままです。
ねじり時の内部力係数
ねじりは、ビームの断面に 1 つの内力要素、つまりトルクのみが現れる荷重です。 外部負荷も2つ
トルク線図
トルクモーメントはビームの軸に沿って変化する可能性があります。 断面に沿ったモーメントの値を決定した後、ビームの軸に沿ったトルクの図を作成します。
ねじり応力
梁の表面に縦線と横線のグリッドを描き、図1の後に表面に形成されるパターンを検討します。 27.1a 変形 (図 27.1a)。 ポップ
最大ねじり応力
応力を決定する式とねじり時の接線方向の応力の分布図から、最大応力が表面で発生することが明らかです。 最大電圧を決めてみましょう
強度計算の種類
強度計算には次の 2 種類があります。 1. 設計計算 - 危険部分のビーム (シャフト) の直径が決定されます。
剛性の計算
剛性を計算する際には、変形量を求めて許容値と比較します。 モーメント t を持つ外部からの力のペアの作用下での丸い梁の変形を考えてみましょう (図 27.4)。
基本的な定義
曲げは、内部力係数 (曲げモーメント) がビームの断面に現れる荷重の一種です。 ビーム作業中
曲げ時の内部力要因
例 1. モーメント m と外力 F を持つ 1 組の力が作用する梁を考えます (図 29.3a)。 内力係数を決定するには、次の方法を使用します。
曲げモーメント
セクション内の横方向の力は、それが回転する傾向がある場合、正であるとみなされます。
直接横曲げに対する差動依存性
曲げモーメント、せん断力、均一強度の間の微分関係を使用することにより、せん断力と曲げモーメントの図の作成が大幅に簡素化されます。
セクションメソッドの使用 結果の式は一般化できます
検討中のセクションの横力は、検討中のセクションまでのビームに作用するすべての力の代数和に等しい: Q = ΣFi
電圧
右側にクランプされ、集中力 F が加わった梁の曲がりを考えてみましょう (図 33.1)。
ある時点でのストレス状態
ある点での応力状態は、この点を通過するすべての領域 (セクション) に発生する垂直応力と接線方向の応力によって特徴付けられます。 通常は、たとえば次のように判断するだけで十分です。
複雑な変形状態の概念
ある点を通過するさまざまな方向およびさまざまな平面で発生する一連の変形によって、この点での変形状態が決まります。 複雑な変形
ねじりを伴う曲げのための丸梁の計算
曲げとねじりの作用下で丸い梁を計算する場合（図34.3）、垂直応力と接線方向の応力を考慮する必要があります。これは、両方の場合で最大応力値が発生するためです。
安定平衡と不安定平衡の概念
比較的短くて大きなロッドは圧縮用に設計されています。 破壊または残留変形の結果として破損します。 アクション用の小さな断面を持つ長いロッド
安定性計算
安定性の計算は、許容圧縮力とそれとの比較における作用力の決定で構成されます。
オイラーの公式による計算
臨界力を決定する問題は、1744 年に L. オイラーによって数学的に解決されました。両側がヒンジで固定されたロッド (図 36.2) の場合、オイラーの公式は次の形式になります。
重大なストレス
臨界応力は臨界力に対応する圧縮応力です。 圧縮力による応力は次の式で求められます。
オイラーの公式の適用限界
オイラーの公式は弾性変形の範囲内でのみ有効です。 したがって、臨界応力は材料の弾性限界よりも小さくなければなりません。 前へ
