Ekuacioni i formës

ku disa numra quhen ekuacion i diferencës lineare me koeficientë konstante.

Zakonisht, në vend të ekuacionit (1), konsiderohet një ekuacion që merret nga (1) duke kaluar nga diferencat e fundme në vlerën e funksionit, d.m.th., një ekuacion të formës.

Nëse ka një funksion në ekuacionin (2), atëherë një ekuacion i tillë quhet homogjen.

Merrni parasysh ekuacionin homogjen

Teoria e ekuacioneve të diferencës lineare është e ngjashme me teorinë e ekuacioneve diferenciale lineare.

Teorema 1.

Nëse funksionet janë zgjidhje të ekuacionit homogjen (3), atëherë funksioni

është gjithashtu një zgjidhje e ekuacionit (3).

Dëshmi.

Le të zëvendësojmë funksionet në (3)

meqenëse funksioni është zgjidhje e ekuacionit (3).

Funksionet e rrjetës quhen të varura linearisht nëse ka numra të tillë që dhe të paktën një është i ndryshëm nga zero, për çdo n është e vërtetë:

(4)

Nëse (4) ndodh vetëm kur atëherë funksionet quhen linearisht të pavarur.

Çdo k zgjidhje e pavarur lineare e ekuacionit (3) formon një sistem themelor zgjidhjesh.

Lërini zgjidhje të pavarura lineare të ekuacionit (3), atëherë

është një zgjidhje e përgjithshme e ekuacionit (3). Kur gjendet një gjendje specifike, ajo përcaktohet nga kushtet fillestare

Ne do të kërkojmë një zgjidhje për ekuacionin (3) në formën:

Le të zëvendësojmë në ekuacionin (3)

Le të pjesëtojmë ekuacionin (5) me

Ekuacioni karakteristik. (6)

Le të supozojmë se (6) ka vetëm rrënjë të thjeshta Është e lehtë ta verifikosh këtë janë linearisht të pavarur. Zgjidhja e përgjithshme e ekuacionit homogjen (3) ka formën

Shembull.

Merrni parasysh ekuacionin

Ekuacioni karakteristik ka formën

Zgjidhja ka formën

Le të ketë rrënja shumësi r. Kjo rrënjë korrespondon me zgjidhjen

Nëse supozojmë se rrënjët e mbetura nuk janë shumëfish, atëherë zgjidhja e përgjithshme e ekuacionit (3) ka formën

Le të shqyrtojmë zgjidhjen e përgjithshme të ekuacionit johomogjen (2).

Një zgjidhje e veçantë për ekuacionin johomogjen (2), pastaj zgjidhja e përgjithshme

LEKTORIA 16

Skica e leksionit

1. Koncepti i D dhe Z - transformimet.

2. Fusha e zbatimit të transformimeve D dhe Z.

3. Shndërrimet e anasjellta D dhe Z.

TRANSFORMI DISKRET LAPLACE.

Z – KONVERSIONI.

Në kërkimet e aplikuara në lidhje me përdorimin e funksioneve të rrjetës, transformimi diskret Laplace (D - transformimi) dhe Z - transformimi janë përdorur gjerësisht. Për analogji me transformimin e zakonshëm të Laplace, transformimi diskrete jepet në formë

ku (1)

Në mënyrë simbolike, D - transformimi shkruhet në formë

Për funksionet e kafazit të kompensuar

ku është kompensimi.

Z – transformimi fitohet nga D – transformim me zëvendësim dhe jepet nga relacioni

(3)

Për një funksion të zhvendosur

Një funksion quhet origjinal nëse

2) ekziston një tregues i rritjes, d.m.th. ka të tillë dhe atë

(4)

Numri më i vogël (ose kufiri në të cilin priret numri më i vogël) për të cilin pabarazia (4) është e vërtetë quhet abshisa e konvergjencës absolute dhe shënohet

Teorema.

Nëse funksioni është origjinal, atëherë imazhi përcaktohet në domenin Re p > dhe është një funksion analitik në këtë fushë.

Le të tregojmë se për Re p > seria (1) është absolutisht konvergjente. ne kemi

meqenëse shuma e treguar është shuma e termave të një progresion gjeometrik në rënie me treguesin Dihet që një progresion i tillë konvergon. Vlera mund të merret si arbitrarisht afër vlerës, d.m.th., pjesa e parë e teoremës vërtetohet.

Pjesën e dytë të teoremës e pranojmë pa prova.

Imazhi është një funksion periodik me një periudhë imagjinare

Kur studioni një imazh, nuk ka kuptim ta konsideroni atë në të gjithë rrafshin kompleks, mjafton të kufizoni studimin në çdo shirit gjersie. e cila quhet kryesore. Se. Mund të supozojmë se imazhet janë përcaktuar në gjysmë-shirit

dhe është një funksion analitik në këtë gjysmëshirit.

Le të gjejmë domenin e përkufizimit dhe analiticitetit të funksionit F(z) duke vendosur . Le të tregojmë se gjysmë-shirit rrafshi p shndërrohet me shndërrim në një rajon në rrafshin z: .

Në të vërtetë, segmenti , duke kufizuar gjysmëshiritin në rrafshin p, përkthehet në rrafshin z në fqinjësi: .

Le të shënojmë me vijën në të cilën shndërrimi merr segmentin . Pastaj

Lagje.

Se. Z – transformimi F(z) është përcaktuar në domen dhe është një funksion analitik në këtë fushë.

Transformimi i kundërt D lejon që dikush të rindërtojë funksionin e rrjetës nga imazhi

(5)

Le të vërtetojmë vlefshmërinë e barazisë.

Shtrihu brenda lagjes.

(7)

(8)

Në barazitë (7) dhe (8), mbetjet merren mbi të gjitha pikat singulare të funksionit F(s).

Zgjidhja e ekuacioneve të zakonshme të diferencës lineare

me koeficientë konstante

Marrëdhënia midis prodhimit dhe hyrjes së një sistemi linear diskret mund të përshkruhet nga një ekuacion i zakonshëm i diferencës lineare me koeficientë konstante

,

Ku y[n]- sinjali i daljes për momentin n,

x[n]- sinjali hyrës për momentin n,

ai,b k– koeficientët konstant.

Dy metoda mund të përdoren për të zgjidhur ekuacione të tilla

• Metoda e drejtpërdrejtë
• Metoda Z – transformimet.

Së pari, le të shqyrtojmë zgjidhjen e një ekuacioni të ndryshimit linear duke përdorur metodën e drejtpërdrejtë.

Zgjidhja e përgjithshme e një ekuacioni të diferencës lineare jo-homogjene (me anën e djathtë jozero) është e barabartë me shumën e zgjidhje e përgjithshme ekuacioni linear i diferencës homogjene dhe zgjidhje private ekuacioni johomogjen

Zgjidhja e përgjithshme e ekuacionit të diferencës homogjene ( zero-hyrjepërgjigje) y h [n]

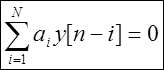
përkufizohet si

.

Duke e zëvendësuar këtë zgjidhje në një ekuacion homogjen, marrim

Një polinom i tillë quhet polinom karakteristik sistemeve. Ai ka N rrënjët . Rrënjët mund të jenë reale ose komplekse dhe disa rrënjë mund të jenë të rastësishme (të shumëfishta).

Nëse rrënjët janë reale dhe të ndryshme, atëherë zgjidhja e ekuacionit homogjen ka formën

ku janë koeficientët

Nëse ndonjë rrënjë, për shembull, λ 1 ka një shumësi m, atëherë termi përkatës i zgjidhjes merr formën

Nëse të gjithë koeficientët e një ekuacioni homogjen dhe, në përputhje me rrethanat, një polinom karakteristik janë real, atëherë dy termat e zgjidhjes që korrespondojnë me rrënjët e thjeshta komplekse të konjuguara mund të paraqitet (shkruhen) në formën , me koeficientët A,B përcaktohen nga kushtet fillestare.

Lloji i zgjidhjes private y p [n] ekuacioni varet nga ana e djathtë (sinjali hyrës) dhe përcaktohet sipas tabelës më poshtë

Tabela 1. Lloji i zgjidhjes së veçantë për karaktere të ndryshme të anës së djathtë

Sinjali i hyrjesx[n]	Zgjidhje privatey p [n]
A(konstante)

Zgjidhja e një ekuacioni të diferencës lineare me metodën e transformimit Z konsiston në përdorimin Z– shndërrimet në një ekuacion duke përdorur vetitë e linearitetit dhe zhvendosjes kohore. Rezultati është një ekuacion algjebrik linear në lidhje me Z- imazhet e funksionit të kërkuar. E kundërta Z– transformimi jep zgjidhjen e dëshiruar në domenin kohor. Për të marrë transformimin e anasjelltë Z, përdoret më shpesh zbërthimi i një shprehjeje racionale në fraksione të thjeshta (elementare), pasi shndërrimi i anasjelltë nga një fraksion elementar i veçantë ka një formë të thjeshtë.

Vini re se për të kaluar në domenin e kohës, mund të përdoren metoda të tjera për llogaritjen e transformimit të kundërt Z.

Shembull. Le të përcaktojmë përgjigjen (sinjalin dalës) të sistemit të përshkruar nga ekuacioni i diferencës lineare ndaj sinjalit hyrës

Zgjidhje.

1. Metoda e drejtpërdrejtë për zgjidhjen e ekuacionit.

Ekuacioni homogjen. Polinom karakteristik i tij.

Rrënjët e një polinomi .

Zgjidhja e një ekuacioni homogjen.

Meqenëse, ne përcaktojmë një zgjidhje të veçantë në formë .

Zëvendësojeni atë në ekuacion

Për të gjetur konstanten TE le të pranojmë n=2. Pastaj

Ose, K=2.33

Prandaj zgjidhja e veçantë dhe zgjidhja e përgjithshme e ekuacionit të diferencës (1)

Le të gjejmë konstantet C 1 Dhe C 2. Për ta bërë këtë, le të vendosim n=0, atëherë nga ekuacioni origjinal i diferencës marrim . Për një ekuacion të dhënë

Kjo është arsyeja pse. Nga shprehja (1)

Prandaj,

.

Nga shprehja (1) për n=1 ne kemi.
Ne marrim dy ekuacionet e mëposhtme për C 1 dhe C 2

.

Zgjidhja e këtij sistemi jep këto vlera: C 1 = 0,486 dhe C 2 = -0,816.

Prandaj, zgjidhja e përgjithshme e këtij ekuacioni është

2. Zgjidhje duke përdorur metodën e transformimit Z.

Le të marrim Z - transformimin nga ekuacioni origjinal i diferencës, duke marrë parasysh vetinë (teoremën) e zhvendosjes kohore . marrim

Shpesh përmendja e thjeshtë e ekuacioneve diferenciale u jep studentëve një ndjenjë të pakëndshme. Pse po ndodh kjo? Më shpesh, sepse kur studiohen bazat e materialit, lind një boshllëk njohurish, për shkak të të cilit studimi i mëtejshëm i shpërndarësve bëhet thjesht torturë. Nuk është e qartë se çfarë të bëni, si të vendosni, ku të filloni?

Sidoqoftë, ne do të përpiqemi t'ju tregojmë se shpërndarësit nuk janë aq të vështirë sa duket.

Konceptet themelore të teorisë së ekuacioneve diferenciale

Nga shkolla i njohim ekuacionet më të thjeshta në të cilat duhet të gjejmë të panjohurën x. Në thelb ekuacionet diferenciale vetëm paksa e ndryshme prej tyre - në vend të një ndryshoreje X ju duhet të gjeni një funksion në to y(x) , e cila do ta kthejë ekuacionin në një identitet.

Ekuacionet diferenciale kanë një rëndësi të madhe praktike. Kjo nuk është matematikë abstrakte që nuk ka asnjë lidhje me botën përreth nesh. Shumë procese të vërteta natyrore përshkruhen duke përdorur ekuacione diferenciale. Për shembull, dridhjet e një vargu, lëvizja e një oshilatori harmonik, duke përdorur ekuacione diferenciale në problemet e mekanikës, gjejnë shpejtësinë dhe nxitimin e një trupi. Gjithashtu DU përdoren gjerësisht në biologji, kimi, ekonomi dhe shumë shkenca të tjera.

Ekuacioni diferencial (DU) është një ekuacion që përmban derivate të funksionit y(x), vetë funksionin, variabla të pavarur dhe parametra të tjerë në kombinime të ndryshme.

Ka shumë lloje ekuacionesh diferenciale: ekuacione diferenciale të zakonshme, lineare dhe jolineare, homogjene dhe johomogjene, ekuacione diferenciale të rendit të parë dhe më të lartë, ekuacione diferenciale të pjesshme etj.

Zgjidhja e një ekuacioni diferencial është një funksion që e kthen atë në një identitet. Ekzistojnë zgjidhje të përgjithshme dhe të veçanta për telekomandën.

Një zgjidhje e përgjithshme për një ekuacion diferencial është një grup i përgjithshëm zgjidhjesh që e shndërrojnë ekuacionin në një identitet. Një zgjidhje e pjesshme e një ekuacioni diferencial është një zgjidhje që plotëson kushtet shtesë të specifikuara fillimisht.

Rendi i një ekuacioni diferencial përcaktohet nga rendi më i lartë i derivateve të tij.

Ekuacionet diferenciale të zakonshme

Ekuacionet diferenciale të zakonshme janë ekuacione që përmbajnë një ndryshore të pavarur.

Le të shqyrtojmë ekuacionin diferencial më të thjeshtë të zakonshëm të rendit të parë. Duket si:

Ky ekuacion mund të zgjidhet thjesht duke integruar anën e djathtë të tij.

Shembuj të ekuacioneve të tilla:

Ekuacione të ndashme

Në përgjithësi, ky lloj ekuacioni duket si ky:

Ja një shembull:

Kur zgjidhni një ekuacion të tillë, duhet të ndani variablat, duke e sjellë atë në formën:

Pas kësaj, mbetet për të integruar të dy pjesët dhe për të marrë një zgjidhje.

Ekuacionet diferenciale lineare të rendit të parë

Ekuacione të tilla duken si:

Këtu p(x) dhe q(x) janë disa funksione të ndryshores së pavarur, dhe y=y(x) është funksioni i dëshiruar. Këtu është një shembull i një ekuacioni të tillë:

Kur zgjidhin një ekuacion të tillë, më së shpeshti përdorin metodën e ndryshimit të një konstante arbitrare ose paraqesin funksionin e dëshiruar si produkt i dy funksioneve të tjera y(x)=u(x)v(x).

Për të zgjidhur ekuacione të tilla, kërkohet një përgatitje e caktuar dhe do të jetë mjaft e vështirë t'i marrësh ato "me një shikim".

Një shembull i zgjidhjes së një ekuacioni diferencial me ndryshore të ndashme

Pra, ne shikuam llojet më të thjeshta të telekomandës. Tani le të shohim zgjidhjen për njërën prej tyre. Le të jetë ky një ekuacion me ndryshore të ndashme.

Së pari, le të rishkruajmë derivatin në një formë më të njohur:

Pastaj i ndajmë variablat, domethënë, në njërën pjesë të ekuacionit mbledhim të gjitha "I-të", dhe në tjetrën - "X"-të:

Tani mbetet për të integruar të dyja pjesët:

Ne integrojmë dhe marrim një zgjidhje të përgjithshme për këtë ekuacion:

Sigurisht, zgjidhja e ekuacioneve diferenciale është një lloj arti. Ju duhet të jeni në gjendje të kuptoni se çfarë lloj ekuacioni është, dhe gjithashtu të mësoni të shihni se çfarë transformimesh duhet të bëhen me të në mënyrë që të çoni në një formë ose në një tjetër, për të mos përmendur vetëm aftësinë për të diferencuar dhe integruar. Dhe për të pasur sukses në zgjidhjen e DE, ju duhet praktikë (si në çdo gjë). Dhe nëse aktualisht nuk keni kohë për të kuptuar se si zgjidhen ekuacionet diferenciale, ose problemi Cauchy ju ka ngecur si një kockë në fyt, ose nuk dini si të përgatisni siç duhet një prezantim, kontaktoni autorët tanë. Në një kohë të shkurtër, ne do t'ju ofrojmë një zgjidhje të gatshme dhe të detajuar, detajet e së cilës mund t'i kuptoni në çdo kohë të përshtatshme për ju. Ndërkohë, ju sugjerojmë të shikoni një video me temën "Si të zgjidhim ekuacionet diferenciale":

Përdorimi i ekuacioneve është i përhapur në jetën tonë. Ato përdoren në shumë llogaritje, ndërtime strukturash dhe madje edhe sporte. Njeriu përdorte ekuacione në kohët e lashta, dhe që atëherë përdorimi i tyre vetëm është rritur. Një ekuacion i diferencës është një ekuacion që lidh vlerën e një funksioni të panjohur në çdo pikë me vlerën e tij në një ose më shumë pika të vendosura në një interval të caktuar nga ai i dhënë. Shembull:

\[Г (z+1) = zГ(z)\]

Për ekuacionet e diferencës me koeficientë konstante, ekzistojnë metoda të detajuara për gjetjen e një zgjidhjeje në formë të mbyllur. Ekuacionet e diferencës johomogjene dhe homogjene të rendit të n-të jepen, përkatësisht, nga ekuacionet ku \ janë koeficientë konstante.

Ekuacionet e diferencës homogjene.

Merrni parasysh ekuacionin e rendit të n-të

\[(a_nE^n +a(n-1)E^n1 + \cpika +a_1E + a_1)y(k) = 0 \]

Zgjidhja e propozuar duhet të kërkohet në formën:

ku \ është një vlerë konstante që duhet përcaktuar. Lloji i zgjidhjes së propozuar të dhënë nga ekuacioni nuk është më i zakonshmi. Vlerat e lejuara të \ shërbejnë si rrënjë të polinomit të \[ e^r.\] Kur \[ \beta = e^r \] zgjidhja e pritur bëhet:

ku \[\beta\] është një vlerë konstante për t'u përcaktuar. Duke zëvendësuar ekuacionin dhe duke marrë parasysh \, marrim ekuacionin karakteristik të mëposhtëm:

Ekuacionet e diferencës johomogjene. Metoda e koeficientëve të papërcaktuar. Le të shqyrtojmë ekuacionin e diferencës së rendit të n-të

\[ (a_nEn +a_(n-1)En^-1+\cdots+ a_1E +a_1)y(k) =F(k) \]

Përgjigja duket si kjo:

Ku mund të zgjidh një ekuacion të diferencës në internet?

Ju mund ta zgjidhni ekuacionin në faqen tonë të internetit https://site. Zgjidhësi falas në internet do t'ju lejojë të zgjidhni ekuacionet në internet të çdo kompleksiteti në disa sekonda. E tëra çfarë ju duhet të bëni është thjesht të futni të dhënat tuaja në zgjidhës. Ju gjithashtu mund të shikoni udhëzime video dhe të mësoni se si ta zgjidhni ekuacionin në faqen tonë të internetit. Dhe nëse keni ende pyetje, mund t'i bëni ato në grupin tonë VKontakte http://vk.com/pocketteacher. Bashkohuni me grupin tonë, ne jemi gjithmonë të lumtur t'ju ndihmojmë.

Hyrje

Në dekadat e fundit, metodat matematikore kanë depërtuar gjithnjë e më shumë në shkencat humane dhe, në veçanti, në ekonomi. Falë matematikës dhe zbatimit efektiv të saj, mund të shpresohet në rritje ekonomike dhe prosperitet të shtetit. Zhvillimi efektiv dhe optimal është i pamundur pa përdorimin e matematikës.

Qëllimi i kësaj pune është të studiojë zbatimin e ekuacioneve të diferencës në sferën ekonomike të shoqërisë.

Kjo punë ka këto detyra: përcaktimin e konceptit të ekuacioneve të diferencës; shqyrtimi i ekuacioneve të diferencës lineare të rendit të parë dhe të dytë dhe zbatimi i tyre në ekonomi.

Gjatë punës në projektin e kursit, u përdorën materialet e disponueshme për studim nga librat shkollorë të ekonomisë, analiza matematikore, vepra të ekonomistëve dhe matematikanëve kryesorë, libra referencë, artikuj shkencorë dhe analitikë të botuar në botime në internet.

Ekuacionet e diferencës

§1. Konceptet bazë dhe shembuj të ekuacioneve të diferencës

Ekuacionet e diferencës luajnë një rol të rëndësishëm në teorinë ekonomike. Shumë ligje ekonomike vërtetohen duke përdorur këto ekuacione. Le të shohim konceptet themelore të ekuacioneve të diferencës.

Le të veprojë koha t si ndryshore e pavarur, dhe ndryshorja e varur përcaktohet për kohën t, t-1, t-2, etj.

Le të shënojmë me vlerën në kohën t; përmes - vlera e funksionit në një moment të zhvendosur me një (për shembull, në orën e mëparshme, në javën e mëparshme, etj.); përmes - vlera e funksionit y në momentin e zhvendosur prapa dy njësi, etj.

Ekuacioni

ku janë konstante, quhet një ekuacion i diferencës johomogjene të rendit të n-të me koeficientë konstante.

Ekuacioni

Në të cilin =0 quhet ekuacion diferencial homogjen i rendit të n-të me koeficientë konstante. Të zgjidhësh një ekuacion të ndryshimit të rendit të n-të do të thotë të gjesh një funksion që e kthen këtë ekuacion në identitetin e saktë.

Zgjidhja në të cilën nuk ka konstante arbitrare quhet zgjidhje e pjesshme e ekuacionit të diferencës; nëse zgjidhja përmban një konstante arbitrare, atëherë ajo quhet zgjidhje e përgjithshme. Teoremat e mëposhtme mund të vërtetohen.

Teorema 1. Nëse ekuacioni i diferencës homogjene (2) ka zgjidhje dhe, atëherë edhe funksioni do të jetë zgjidhje

ku dhe janë konstante arbitrare.

Teorema 2. Nëse është një zgjidhje e veçantë e ekuacionit të diferencës johomogjene (1) dhe është zgjidhja e përgjithshme e ekuacionit homogjen (2), atëherë zgjidhja e përgjithshme e ekuacionit johomogjen (1) do të jetë funksioni

Konstante arbitrare. Këto teorema janë të ngjashme me ato për ekuacionet diferenciale. Një sistem i ekuacioneve të diferencës lineare të rendit të parë me koeficientë konstante është një sistem i formës

ku është një vektor i funksioneve të panjohura, është një vektor i funksioneve të njohura.

Ekziston një matricë e madhësisë nn.

Ky sistem mund të zgjidhet duke e reduktuar atë në një ekuacion të ndryshimit të rendit të n-të me analogji me zgjidhjen e një sistemi ekuacionesh diferenciale.

§ 2. Zgjidhja e ekuacioneve të diferencës

Zgjidhja e një ekuacioni të diferencës së rendit të parë. Merrni parasysh ekuacionin e diferencës johomogjene

Ekuacioni përkatës homogjen është

Le të kontrollojmë nëse funksioni do të jetë

zgjidhja e ekuacionit (3).

Duke zëvendësuar në ekuacionin (4), marrim

Prandaj, ekziston një zgjidhje për ekuacionin (4).

Zgjidhja e përgjithshme e ekuacionit (4) është funksioni

ku C është një konstante arbitrare.

Le të jetë një zgjidhje e veçantë e ekuacionit johomogjen (3). Atëherë zgjidhja e përgjithshme e ekuacionit të diferencës (3) është funksioni

Le të gjejmë një zgjidhje të veçantë për ekuacionin e diferencës (3) nëse f(t)=c, ku c është një variabël.

Ne do të kërkojmë një zgjidhje në formën e një konstante m. ne kemi

Zëvendësimi i këtyre konstanteve në ekuacion

marrim

Prandaj, zgjidhja e përgjithshme e ekuacionit të diferencës

Shembull 1. Duke përdorur një ekuacion të diferencës, gjeni formulën për rritjen e depozitës në para të gatshme A në bankën e kursimeve, të depozituar në p% në vit.

Zgjidhje. Nëse një shumë e caktuar depozitohet në një bankë me interes të përbërë p, atëherë deri në fund të vitit shuma e saj do të jetë

Ky është një ekuacion i diferencës homogjene të rendit të parë. Vendimi i tij

ku C është një konstante që mund të llogaritet nga kushtet fillestare.

Nëse pranojmë, atëherë C=A, prej nga

Kjo është një formulë e njohur për llogaritjen e rritjes së një depozite në para të vendosura në një bankë kursimi me një normë interesi të përbërë.

Zgjidhja e një ekuacioni të diferencës së rendit të dytë. Le të shqyrtojmë një ekuacion të diferencës johomogjene të rendit të dytë

dhe ekuacioni homogjen përkatës

Nëse k është rrënja e ekuacionit

është një zgjidhje e ekuacionit homogjen (6).

Në të vërtetë, duke zëvendësuar në anën e majtë të ekuacionit (6) dhe duke marrë parasysh (7), marrim

Kështu, nëse k është rrënja e ekuacionit (7), atëherë është zgjidhje e ekuacionit (6). Ekuacioni (7) quhet ekuacioni karakteristik për ekuacionin (6). Nëse ekuacioni i karakteristikës diskriminuese (7) është më i madh se zero, atëherë ekuacioni (7) ka dy rrënjë reale të ndryshme dhe, dhe zgjidhja e përgjithshme e ekuacionit homogjen (6) ka formën e mëposhtme.