Leçon et présentation sur le sujet :
Matériaux additionnels
Chers utilisateurs, n'oubliez pas de laisser vos commentaires, avis, souhaits ! Tous les documents ont été vérifiés par un programme antivirus.
Supports pédagogiques et simulateurs dans la boutique en ligne Integral pour la 11e année
Problèmes algébriques avec paramètres, niveaux 9 à 11
Environnement logiciel "1C : Constructeur Mathématique 6.1"
Les gars, nous devons simplement considérer une autre méthode pour résoudre les équations - fonctionnelle-graphique. L'essence de la méthode est simple et nous l'avons déjà utilisée.
Donnons-nous une équation de la forme $f(x)=g(x)$. Nous construisons deux graphiques $y=f(x)$ et $y=g(x)$ sur le même plan de coordonnées et marquons les points d'intersection de nos graphiques. L'abscisse du point d'intersection (coordonnée x) est la solution de notre équation.
La méthode étant dite fonctionnelle-graphique, il n'est pas toujours nécessaire de construire des graphiques de fonctions. Vous pouvez également utiliser les propriétés des fonctions. Par exemple, vous voyez une solution explicite à une équation à un moment donné : si l’une des fonctions est strictement croissante et l’autre strictement décroissante, alors ce sera la seule solution de l’équation. Les propriétés de monotonie des fonctions aident souvent à résoudre diverses équations.
Rappelons une autre méthode : si sur l'intervalle X, la plus grande valeur de l'une des fonctions $y=f(x)$, $y=g(x)$ est égale à A, et, par conséquent, la plus petite valeur de l'autre fonction est également égale à A, alors l'équation $f( x)=g(x)$ est équivalente au système : $\begin (cases) f(x)=A, \\ g(x)=A . \fin (cas)$
Exemple.
Résolvez l'équation : $\sqrt(x+1)=|x-1|$.
Solution.
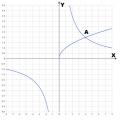
Construisons des graphiques de fonctions sur le même plan de coordonnées : $y=\sqrt(x)+1$ et $y=|x-1|$.
Comme le montre la figure, nos graphiques se croisent en deux points de coordonnées : A(0;1) et B(4;3). La solution de l’équation originale sera les abscisses de ces points.
Réponse : $x=0$ et $x=4$.
Exemple.
Résolvez l'équation : $x^7+3x-134=0$.
Solution.
Passons à l'équation équivalente : $x^7=134-3x$.
Vous pouvez voir que $x=2$ est une solution à cette équation. Montrons que c'est la seule racine.
Fonction $y=x^7$ – augmente dans tout le domaine de définition.
Fonction $y=134-3x$ – diminue sur tout le domaine de définition.
Alors les graphiques de ces fonctions soit ne se coupent pas du tout, soit se coupent en un point, nous avons déjà trouvé ce point $x=2.$
Réponse : $x=2$.
Exemple.
Résolvez l'équation : $\frac(8)(x)=\sqrt(x)$.
Solution.
Cette équation peut être résolue de deux manières.
1. Encore une fois, notez que $x=4$ est la racine de l'équation. Sur le segment $)