Многогранник состоящий из многоугольника называемого основанием. Понятие многогранника

Это такое тело, поверхность которого состоит из конечной числа плоских многоугольников. Многогранник называется выпуклым , если он лежит по одну сторону от плоскости каждой из плоских многоугольников на его поверхности. Общая часть такой плоскости и поверхности выпуклого многоугольника называется гранью .
На рисунке ниже слева изображен неопуклий многогранник; на рисунке справа - выпуклый.

Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника , а вершины граней - вершинами многогранника .

Призма

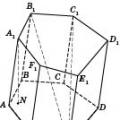
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (см. рисунок). Многоугольники называются основаниями призмы , а отрезки, соединяющие соответствующие вершины - боковыми ребрами призмы .

Обозначения: .
Боковая поверхность призмы состоит из параллелограммов. Каждый из них имеет две стороны, которые являются соответствующими сторонами основания, а две другие - смежными боковыми ребрами. Основания призмы равны и лежат в параллельных плоскостях. Боковые ребра призмы параллельны и равны. Высотой призмы называется расстояние между плоскостями ее оснований.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы . (На рисунке - высота, и диагонали.)
Диагональные сечения - это сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани (см. рисунки).

Призма называется прямой , если ее боковые ребра перпендикулярны к основаниям. В противном случае призма называется наклонной .
Боковые грани прямой призмы - прямоугольники, высота прямой призмы равна боковому ребру, диагональные сечения являются прямоугольниками.
Боковой поверхностью призмы называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 1. Боковая поверхность прямой призмы равна произведению периметра основания и высоты, то есть длины бокового ребра.
Перпендикулярным сечением призмы будем называть сечение плоскостью, перпендикулярной боковому ребру призмы (а это значит, что эта плоскость является перпендикулярной всех боковых ребер призмы).
Теорема 2. Боковая поверхность наклонной призмы равна произведению длины бокового ребра и периметра перпендикулярного сечения.
На рисунке - перпендикулярное сечение.
S б = H ⋅ P осн;
S п = S б + 2S осн.
S б = l ⋅ P тэр;
S п = S б + 2S осн.

Очевидно, что эта теорема верна и в случае прямой призмы, потому что тогда перпендикулярное сечение будет сечением плоскостью, параллельной плоскостям оснований призмы.
Обратите внимание: если некоторый многоугольник является перпендикулярным сечением призмы, то его внутренние углы являются линейными углами двугранных углов между соответствующими боковыми гранями.
В случае прямой призмы линейными углами двугранных углов между боковыми гранями являются непосредственно углы основания.
Пример
На рисунке - прямая призма.

- линейный угол двугранного угла между гранями и .
Призма называется правильной , если:
в основе ее лежит правильный многоугольник;
призма является прямой.

Параллелепипед

Собой параллелепипед называется призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда - параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противоположными .
Теорема 1. Противоположные грани параллелепипеда являются параллельными и ровными.
Параллелепипед остается собой параллелепипед во всех случаях, когда за его основу считаем любую его грань (см. рисунок).
Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Из этого следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии.
Обратите внимание: у прямого параллелепипеда имеются четыре диагонали, которые попарно равны друг другу.
На рисунке ; .
Это следует из свойств наклонных, так - равные перпендикуляры к плоскости основания ABCD.

Если две диагонали прямого параллелепипеда выходящие из соседних вершин, то большая из них та, которая проектируется в большую диагональ основания, то есть такую диагональ параллелограмма, которая лежит против тупого угла. Следовательно, если на приведенном выше рисунке считать угол ABC тупой, получим , .
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным собой параллелепипед (см. рисунок).

Все грани прямоугольного параллелепипеда - прямоугольники, которые можно разбить на три пары равных между собой. Произвольную грань прямоугольного параллелепипеда можно считать его основой. Учитывая, что при параллельном проектировании произвольный параллелограмм может изображаться произвольным параллелограммом, изображение прямоугольного параллелепипеда никак не отличается от изображения любого прямого параллелепипеда.
Длины непараллельных ребер называются линейными размерами (измерениями) прямоугольного параллелепипеда.
Теорема 3. В прямоугольном параллелепипеде все диагонали равны. Квадрат диагонали равен сумме квадратов трех его измерений.
Все двугранные углы прямоугольного параллелепипеда являются прямыми.
Прямоугольный параллелепипед имеет три пары равных между собой диагональных сечений. Каждый из этих сечений является прямоугольником (см. рисунки).

Каждая пара сечений пересекаются по прямой, проходящей через точки пересечения диагоналей противоположных граней. Отрезки между этими точками являются параллельными и равны одному из ребер прямоугольного параллелепипеда.
Прямоугольным треугольник, который образуется диагональю прямоугольного параллелепипеда, диагональю боковой грани и стороной основания (см. рисунок). Например, .

Прямоугольный параллелепипед имеет центр симметрии - это точка пересечения его диагоналей.
Он также имеет три плоскости симметрии, проходящие через центр симметрии параллельно граням.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом .
Плоскость любого диагонального сечения куба является его плоскостью симметрии. Таким образом, куб имеет девять плоскостей симметрии.
На рисунке рассмотрим взаимное расположение некоторых элементов прямого параллелепипеда:

- угол между диагональю боковой грани и плоскостью основания ( - перпендикуляр, - наклонная, СD - проекция).
- угол между диагональю прямого параллелепипеда и плоскостью основания ( - перпендикуляр, - наклонная, АС - проекция).
- угол наклона диагонали к боковой грани (AD - перпендикуляр, - наклонная, - проекция).
Пусть - прямой параллелепипед (см. рисунок), где ABCD - ромб. Проведем его сечение плоскостью, проходящей через диагональ основания BD и вершину .

В сечении получим равнобедренный треугольник .
- линейный угол двугранного угла между плоскостями основания и сечения. по свойству диагоналей ромба, - перпендикуляр, - наклонная, СО - проекция. По теореме о трех перпендикуляры: .

Пирамида

Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами .
Высота пирамиды - перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида называетсяn -угольной , если ее основанием является n -угольник. Треугольная пирамида называется также тетраэдром . Боковая грань пирамиды - треугольник. Одной из его вершин является вершина пирамиды, а противоположной стороной - сторона основания пирамиды.
На рисунке SO - высота пирамиды. Тогда - угол между боковым ребром и плоскостью основания (SO - перпендикуляр, SА - наклонная, ОА - проекция).

Из основания высоты пирамиды (точки В ) проведем перпендикуляр на сторону основания (например, АЕ ). Основание этого перпендикуляра (точка F ) соединим с вершиной пирамиды (точка S ). По теореме о трех перпендикуляры: . (SO - перпендикуляр, SP - наклонная, OF - проекция, по построению.) Следовательно, - линейный угол двугранного угла между плоскостью боковой грани ASE и плоскостью основания.
Для решения задач о пирамиде очень важно выяснять, где размещена основа ее высоты.
1. Если выполняется хотя бы одно из следующих условий:
все боковые ребра пирамиды равны;
все боковые ребра наклонены к плоскости основания под одним и тем же углом;
все боковые ребра образуют одинаковые углы с высотой пирамиды;
все боковые ребра равноудалены от основания высоты, то основанием высоты пирамиды является центр окружности, описанной вокруг основания пирамиды.
Боковое ребро l , высота H и радиус R описанной вокруг основания окружности образуют прямоугольный треугольник:

В этом случае боковую поверхность можно найти по формуле , где l - длина бокового ребра, , ... - плоские углы при вершине.
2. Если выполняется хотя бы одно из следующих условий:
все боковые грани наклонены к плоскости основания под одним и тем же углом;
все боковые грани имеют одинаковые высоты;
высоты боковых граней образуют одинаковые углы с высотой пирамиды;
боковые грани равноудалены от основания высоты, - то основание высоты лежит в центре круга, вписанного в основание пирамиды.
На рисунке - прямоугольный , - радиус вписанной окружности в ABCDEF ;

- высота пирамиды, SP - высота боковой грани;
- линейный угол двугранного угла между боковой гранью и плоскостью основания;
О - центр вписанного в основание круга, то есть точка пересечения биссектрис ABCDEF .
В этом случае .
3. Если боковое ребро перпендикулярно к плоскости основания, то это ребро является высотой пирамиды (см. рисунки).

В этом случае и - углы наклона боковых ребер SВ и SС соответственно к плоскости основания. является линейным углом двугранного угла между боковыми гранями SAC и SBA .

4. Если боковая грань перпендикулярна плоскости основания (см. рисунок), то высотой пирамиды будет высота этой грани (по теореме «Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к прямой их пересечения, то она перпендикулярна второй плоскости»).
5. Если две боковые грани перпендикулярны к плоскости основания, то высотой пирамиды является их общее боковое ребро.

Расстояния от основания высоты пирамиды

Расстояние от основания высоты пирамиды до бокового ребра - перпендикуляр, опущенный из точки О на это ребро (см. рисунок). Обратите внимание: , но на рисунке не должен быть прямым: углы при параллельном проектировании не сохраняются.
OF - расстояние от основания высоты до бокового ребра SE ;
ON - расстояние от основания высоты до боковой грани ASB (о это расстояние подробнее смотри ниже).

, где - угол между ребром SE и плоскостью основания.

Расстояние от основания высоты до боковой грани

Пусть , тогда по теореме о трех перпендикуляры. Следовательно, AB перпендикулярна к плоскости SOK . Отсюда, если , то ON перпендикулярна к плоскости ASB .
.
Пирамида называется правильной , если ее основанием является правильный многоугольник, а основание высоты совпадает с центром многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны, боковые грани - равные равнобедренные треугольники. Высота боковой грани, проведенная из вершины пирамиды, называется апофемою . Она является биссектрисой и медианой боковой грани, поскольку та является равнобедренным треугольником.
Теорема. Боковая поверхность правильной пирамиды равна произведению півпериметра основания на апофему.
; ,
где Р - периметр основания, а - сторона основания, l - длина апофеми.
Правильная треугольная пирамида
В основании правильной треугольной пирамиды лежит равносторонний треугольник, который изображается произвольным треугольником (см. рисунок).

Центром является точка пересечения его биссектрис, которые одновременно являются высотами и медіанами. Медианы при параллельном проектировании изображаются медіанами. Поэтому строим две медианы основания. Точка их пересечения - основание высоты пирамиды. Изображаем высоту, а затем соединяем вершину пирамиды с вершинами основания. Получим боковые ребра.
На рисунке: - угол наклона бокового ребра к плоскости основания (одинаковый для всех ребер); - угол наклона боковой грани к плоскости основания (одинаковый для всех граней).
Пусть .
Тогда ; ; ;
; ; .
Следовательно, .
; .
Плоскость осевого сечения ASD является плоскостью симметрии правильной треугольной пирамиды.
Эта плоскость перпендикулярна к плоскости основания и плоскости грани BSC .
Интересно также отметить, что скрещивающиеся ребра пирамиды (SA и BC , SB и AC , SC и AB ) являются перпендикулярными. Если , то ON является расстоянием от основания высоты не только к анафеме, но и к боковой грани BSC .
.
Правильная четырехугольная пирамида
В основании правильной четырехугольной пирамиды лежит квадрат, который изображается произвольным параллелограммом. Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
Пусть сторона квадрата а (см. рисунок).
Тогда ;
;
;
;
.

Обратите внимание: , , то есть .
При параллельном проектировании сохраняется параллельность.
; .
Расстояние от основания высоты до боковой грани:
; .

Правильная шестиугольная пирамида
В основе правильной шестиугольной пирамиды лежит правильный шестиугольник (см. рисунок). Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
Тогда ;
Пусть сторона правильного шестиугольника а .
;
;

.
; .

Усеченная пирамида
Срезанной пирамидой называется многогранник, который останется, если от пирамиды отделить плоскостью, параллельной основе, пирамиду с той же вершиной.
Теорема. Плоскость, которая параллельна основе пирамиды и пересекает ее, отсекает подобную пирамиду.
Обратите внимание: чтобы правильно изобразить срезанную пирамиду, надо начинать с изображения исходной полной пирамиды (см. рисунок).

Основания усеченной пирамиды - подобные многоугольники. Боковые грани - трапеции. - высота усеченной пирамиды, - высота боковой грани, - угол наклона бокового ребра к плоскости основания (любой), - угол наклона боковой грани к плоскости нижнего основания.
Правильная усеченная пирамида - это усеченная пирамида, которую достали из правильной пирамиды.
Ее боковые ребра равны и наклонены к плоскости основания под одним и тем же углом. Ее боковые грани равны рівнобічній трапеции и наклонены к плоскости нижнего основания под одним и тем же углом. Высоты боковых граней пирамиды называются апофемами .
Боковая поверхность правильной усеченной пирамиды равна произведению половину суммы периметров оснований и апофеми.
, где P н и P - периметры соответствующих оснований, l - апофема.
На рисунках изображены фигуры, которые бывает очень полезным рассмотреть при решении задач на срезанную пирамиду.
;
.

;

- прямоугольная трапеция.
- высота усеченной пирамиды.
- высота боковой грани.

В случае, когда усеченная пирамида правильная, отрезки OD и являются радиусами описанной окружности, а OF и - радиусами вписанной окружности для нижней и верхней основы соответственно.

Правильные многогранники

Выпуклый многогранник называется правильным , если его грани являются правильными многогранниками с одним и тем же числом сторон и в каждой вершине многогранника совпадает одно и то же число ребер.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
1. У правильного тетраэдра грани - правильные треугольники; в каждой вершине совпадает по три ребра. Тетраэдр - треугольная пирамида, все ребра которой равны.
2. У куба все грани - квадраты; в каждой вершине совпадает по три ребра. Куб - прямоугольный параллелепипед с равными ребрами.
3. В октаэдра грани - правильные треугольники. В каждой его вершине совпадает по четыре ребра.
4. В додекаедра грани - правильные п"ятикутники. В каждой его вершине совпадает по три ребра.
5. В грани икосаэдра - правильные треугольники. В каждой его вершине совпадает по пять ребер.
На рисунках приведены примеры правильных многогранников с названиями.

Хотя стереометрию изучают только в старших классах школы, но с кубом, правильными пирамидами и другими простыми многогранниками знаком каждый школьник. Тема «Многогранники» имеет яркие приложения, в том числе в живописи и архитектуре. Кроме этого, в ней, по образному выражению академика Александрова, сочетаются «лёд и пламень», то есть живое воображение и строгая логика. Но в школьном курсе стереометрии мало времени уделяется правильным многогранникам. А ведь у многих правильные многогранники вызывают большой интерес, но нет возможности узнать о них больше на уроке. Именно поэтому я решила рассказать обо всех правильных многогранниках, имеющих разнообразные формы, и об их интересных свойствах.

Структура правильных многогранников очень удобна для изучения множества преобразований многогранника в себя (повороты, симметрии и т. д.). Получающиеся при этом группы преобразований (их называют группами симметрии) оказались весьма интересными с точки зрения теории конечных групп. Эта же симметричность позволила создать серию головоломок в виде правильных многогранника, начавшуюся «кубиком Рубиком» и «молдавской пирамидкой».

Для составления реферата использовался Научно-популярный физико-математический журнал «Квант», из которого взята информация о том, что такое правильный многогранник, об их количестве, о построении всех правильных многогранников и описании всех поворотов, при которых многогранник совмещается со своим первоначальным положением. Из газеты «Математика» я получила интересные сведения о звёздчатых правильных многогранниках, их свойствах, открытии и их применении.

Теперь у вас есть возможность окунуться в мир правильного и великолепного, в мир прекрасного и необычайного, который привораживает наш взор.

1. Правильные многогранники

1. 1 Определение правильных многогранников.

Выпуклый многогранник называется правильным, если его гранями являются равные правильные многогранники и все многогранные углы равны.

Рассмотрим возможные правильные многогранники и, прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники. В каждой её вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также правильным тетраэдром, или просто тетраэдром, что в переводе с греческого языка означает четырёхгранник.

Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится четыре грани, его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.

Многогранник, в каждой вершине которого сходиться пять правильных треугольников. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.

Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильных треугольников, то других правильных многоугольников, гранями которых являются правильные треугольники, не существует.

Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба, других правильных многогранников, у которых гранями являются квадраты, не существует. Куб имеет шесть граней и поэтому также называется гексаэдром.

Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходятся три грани. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.

Из определения правильного многогранника следует, что правильный многогранник «совершенно симметричный»: если отметить какую-то грань Г и одну из её вершин А, то для любой другой грани Г1 и её вершины А1 можно совместить многогранник с самим собой движением в пространстве так, что грань Г совместится с Г1 и при этом вершина А попадает в точку А1.

1. 2. Историческая справка.

Пять перечисленных выше правильных многогранников, часто называемых также «телами Платона», захватили воображение математиков, мистиков и философов древности более двух тысяч лет назад. Древние греки даже установили мистическое соответствие между тетраэдром, кубом, октаэдром и икосаэдром и четырьмя природными началами – огнем, землей, воздухом и водой. Что касается пятого правильного многогранника, додекаэдра, то они рассматривали его как форму Вселенной. Эти идеи не являются одним лишь достоянием прошлого. И сейчас, спустя два тысячелетия, многих привлекает лежащее в их основе эстетическое начало.

Первые четыре многогранника были известны задолго до Платона. Археологи нашли додекаэдр, изготовленный во времена этрусской цивилизации по крайней мере за 500 лет до н. э. Но, видимо, в школе Платона додекаэдр был открыт самостоятельно. Существует легенда об ученике Платона Гиппазе, погибшем в море потому, что он разгласил тайну о «шаре с двенадцатью пятиугольниками».

Со времен Платона и Евклида хорошо известно, что существует ровно пять типов правильных многогранников.

Докажем этот факт. Пусть все грани некоторого многогранника -правильные п-угольники и k - число граней, примыкающих к вершине (оно одинаково для всех вершин). Рассмотрим вершину А нашего многогранника. Пусть M1, М2,. , Mk - концы k выходящих из неё рёбер; поскольку двугранные углы при этих рёбрах равны, AM1M2Mk - правильная пирамида: при повороте на угол 360º/k вокруг высоты АН вершина М переходит в М, вершина M1 - в М2. Mk в M1 .

Сравним равнобедренные треугольники AM1M2 и HM1M2 У них основание общее, а боковая сторона AM1 больше HM1, поэтому M1AM2

Тетраэдр 3 3 4 4 6

Куб 4 3 8 6 12

Октаэдр 3 4 6 8 12

Додекаэдр 5 3 20 12 30

Икосаэдр 3 5 12 20 30

1. 3. Построение правильных многогранников.

Все соответствующие многогранники можно построить, взяв за основу куб.

Чтобы получить правильный тетраэдр, достаточно взять четыре несмежные вершины куба и отрезать от него пирамидки четырьмя плоскостями, каждая из которых проходит через три из взятых вершин

Такой тетраэдр можно вписать в куб двумя способами.

Пересечение двух таких правильных тетраэдров - это как раз правильный октаэдр: многогранник из восьми треугольников с вершинами, расположенными в центрах граней куба.

2. Свойства правильных многогранников.

2. 1. Сфера и правильные многогранники.

Вершины любого правильного многогранника лежат на сфере (что вряд ли вызовет удивление, если вспомнить, что вершины любого правильного многоугольника лежат на окружности). Помимо этой сферы, называемой «описанной сферой», имеются еще две важные сферы. Одна из них, «срединная сфера», проходит через середины всех ребер, а другая, «вписанная сфера», касается всех граней в их центрах. Все три сферы имеют общий центр, который называется центром многогранника.

Радиус описанной сферы Название многогранника Радиус вписанной сферы

Тетраэдр

Додекаэдр

Икосаэдр

2. 1. Самосовмещения многогранников.

Какие самосовмещения (вращения, переводящие в себя) есть у куба, тетраэдра и октаэдра? Заметим, что некоторая точка-центр многогранника - при любом самосовмещении переходит в себя, так что все самосовмещения имеют общую неподвижную точку.

Посмотрим, какие вообще в пространстве бывают вращения с неподвижной точкой А. Покажем, что такое вращение обязательно является поворотом на некоторый угол вокруг некоторой прямой проходящей через точку А. Достаточно у нашего движения F(c F(A) = A) указать неподвижную прямую. Найти её можно так: рассмотрим три точки M1, M2 = F(M1) и M3 = F(M2), отличные от неподвижной точки А, проведём через них плоскость и опустим на неё перпендикуляр АН - это и будет искомая прямая. (Если М3 = М1, то наша прямая проходит через середину отрезка M1M2, a F - осевая симметрия: поворот на угол 180°).

Итак, самосовмещение многогранника обязательно является поворотом вокруг оси, проходящей через центр многогранника. Эта ось пересекает наш многогранник в вершине или во внутренней точке ребра или грани. Следовательно, наше самосовмещение переводит в себя вершину, ребро или грань, значит, оно переводит в себя вершину, середину ребра или центр грани. Вывод: движение куба, тетраэдра или октаэдра, совмещающее его с собой, есть вращение вокруг оси одного из трёх типов: центр многогранника - вершина, центр многогранника - середина ребра, центр многогранника - центр грани.

Вообще, если многогранник совмещается с самим собой при повороте вокруг прямой на угол 360°/m, то эту прямую называют осью симметрии m-го порядка.

2. 2. Движение и симметрии.

Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают.

Рассматривая самосовмещения многогранников, можно включить в их число не только вращения, но и любые движения, переводящие многогранник в себя. Здесь движение - это любое преобразование пространства, сохраняющее попарные расстояния между точками.

В число движений, кроме вращений, нужно включить и зеркальные движения. Среди них - симметрия относительно плоскости (отражение), а также композиция отражения относительно плоскости и поворота вокруг перпендикулярной ей прямой (это - общий вид зеркального движения, имеющего неподвижную точку). Конечно, такие движения нельзя реализовать непрерывным перемещением многогранника в пространстве.

Рассмотрим подробнее симметрии тетраэдра. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра. Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии.

Прямые симметрии остальных правильных многогранников можно вычислить по формуле [(q - 1)N0 + N1 + (p - 1)N2]/2 + 1, где р-число сторон правильных многоугольников, являющихся гранями многогранника, q – число граней, примыкающих к каждой вершине, N0 – число вершин, N1 – число ребер и N2 – число граней каждого многогранника.

Гексаэдр и октаэдр имеют по 24 симметрии, а икосаэдр и додекаэдр– по 60 симметрий.

Все правильные многогранники имеют плоскости симметрии (у тетраэдра их - 6, у куба и октаэдра - по 9, у икосаэдра и додекаэдра - по 15).

2. 3. Звёздчатые многогранники.

Кроме правильных многогранников красивые формы имеют звёздчатые многогранники. Их всего четыре. Первые два были открыты И. Кеплером (1571 - 1630), а два других почти 200 лет спустя построил Л. Пуансо (1777 - 1859). Именно поэтому правильные звёздчатые многогранники называются телами Кеплера - Пуансо. Они получаются из правильных многогранников продолжением их граней или рёбер. Французский геометр Пуансо в 1810 году построил четыре правильных звёздчатых многогранника: малый звёздчатый додекаэдр, большой звёздчатый додекаэдр, большой додекаэдр и большой икосаэдр. У этих четырёх многогранников грани - пересекающиеся правильные многогранники, а у двух из них каждая из граней представляет собой самопересекающийся многоугольник. Но Пуансо не сумел доказать, что других правильных многогранников не существует.

Спустя год (в 1811г.) это сделал французский математик Огюстен Луи Коши (1789 - 1857). Он воспользовался тем, что согласно определению правильного многогранника, его можно наложить на самого себя так, что произвольная его грань совместится с наперёд выбранной. Из этого следует, что все грани звёздчатого многогранника равноудалены от некоторой точки-центра сферы, вписанной в многогранник.

Плоскости граней звёздчатого многогранника, пересекаясь, образуют ещё и правильный выпуклый многогранник, то есть платоново тело, описанное около той же сферы. Это платоново тело Коши назвал ядром данного звёздчатого многогранника. Тем самым звёздчатый многогранник можно получить, продолжая плоскости граней одного из платоновых тел.

Из тетраэдра, куба и октаэдра звёздчатые многогранники получить нельзя. Рассмотрим додекаэдр. Продолжение его рёбер приводит к замене каждой грани, звёздчатым правильным пятиугольником, а в результате получается малый звёздчатый додекаэдр.

На продолжении граней додекаэдра возможны следующие два случая: 1) если рассматривать правильные пятиугольники, то получается большой додекаэдр.

2) если же в качестве граней рассматривать звёздчатые пятиугольники, то получается большой звёздчатый додекаэдр.

Икосаэдр имеет одну звёздчатую форму. При продолжении грани правильного икосаэдра получается большой икосаэдр.

Таким образом, существует четыре типа правильных звёздчатых многогранников.

Звёздчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений.

Многие формы звёздчатых многогранников подсказывает сама природа. Снежинки – это звёздчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Заключение

В работе раскрыты следующие темы: правильные многогранники, построение правильных многогранников, самосовмещение, движение и симметрии, звёздчатые многогранники и их свойства. Мы узнали, что существует всего лишь пять правильных многогранника и четыре звёздчатых правильных многогранника, которые нашли широкое применение в различных областях.

Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

Структура правильных многогранников очень удобна для изучения множества преобразований многогранника в себя (повороты, симметрии и т. д.). Получающиеся при этом группы преобразований (их называют группами симметрии) оказались весьма интересными с точки зрения теории конечных групп. Эта же симметричность позволила создать серию головоломок в виде правильных многогранников, начавшуюся «кубиком Рубиком» и «молдавской пирамидкой».

Большой интерес к формам правильных многогранников проявляли также скульпторы, архитекторы, художники. Их всех поражало совершенство, гармония многогранников. Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.

Содержание статьи

МНОГОГРАННИК, часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников. Эти многоугольники называются гранями, их стороны – ребрами, а вершины – вершинами многогранника.

На рис. 1 представлены несколько известных многогранников. Первые два служат примерами р -угольных пирамид, т.е. многогранников, состоящих из р -угольника, называемого основанием, и р треугольников, примыкающих к основанию и имеющих общую вершину (называемую вершиной пирамиды). При р = 3 (см . рис. 1,а ) основанием может служить любая грань пирамиды. Пирамида, основание которой имеет форму правильного р -угольника, называется правильной р -угольной пирамидой. Так, можно говорить о квадратных, правильных пятиугольных и т.д. пирамидах. На рис. 1,в , 1,г и 1,д приведены примеры некоторого класса многогранников, вершины которых можно разделить на два множества из одинакового числа точек; точки каждого из этих множеств являются вершинами р -угольника, причем плоскости обоих p -угольников параллельны. Если эти два р -угольника (основания) конгруэнтны и расположены так, что вершины одного р р -угольника параллельными прямолинейными отрезками, то такой многогранник называется р -угольной призмой. Примерами двух р -угольных призм могут служить треугольная призма (р = 3) на рис. 1,в и пятиугольная призма (р = 5) на рис. 1,г . Если же основания расположены так, что вершины одного р -угольника соединены с вершинами другого р -угольника зигзагообразной ломаной, состоящей из 2р прямолинейных отрезков, как на рис. 1,д , то такой многогранник называется р -угольной антипризмой.

Кроме двух оснований, у р -угольной призмы имеются р граней – параллелограммов. Если параллелограммы имеют форму прямоугольников, то призма называется прямой, а если к тому же основаниями служат правильные р -угольники, то призма называется прямой правильной р -угольной призмой. р -угольная антипризма имеет (2p + 2) граней: 2р треугольных граней и два p -угольных основания. Если основаниями служат конгруэнтные правильные р -угольники, а прямая, соединяющая их центры, перпендикулярна их плоскостям, то антипризма называется прямой правильной р -угольной антипризмой.

В определении многогранника последняя оговорка сделана для того, чтобы исключить из рассмотрения такие аномалии, как две пирамиды с общей вершиной. Теперь мы введем дополнительное ограничение множества допустимых многогранников, потребовав, чтобы никакие две грани не пересекались, как на рис. 1,е . Любой многогранник, удовлетворяющий этому требованию, делит пространство на две части, одна из которых конечна и называется «внутренней». Другая, оставшаяся часть, называется внешней.

Многогранник называется выпуклым, если ни один прямолинейный отрезок, соединяющий любые две его точки, не содержит точек, принадлежащих внешнему пространству. Многогранники на рис. 1,а , 1,б , 1,в и 1,д выпуклые, а пятиугольная призма на рис. 1,г не выпуклая, так как, например, отрезок PQ содержит точки, лежащие во внешнем пространстве призмы.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Выпуклый многогранник называется правильным, если он удовлетворяет следующим двум условиям:

283(i) все его грани – конгруэнтные правильные многоугольники;

(ii) к каждой вершине примыкает одно и то же число граней.

Если все грани – правильные р -угольники и q из них примыкают к каждой вершине, то такой правильный многогранник обозначается {p , q }. Это обозначение было предложено Л.Шлефли (1814–1895), швейцарским математиком, которому принадлежит немало изящных результатов в геометрии и математическом анализе.

Существуют невыпуклые многогранники, у которых грани пересекаются и которые называются «правильными звездчатыми многогранниками». Так как мы условились такие многогранники не рассматривать, то под правильными многогранниками мы будем понимать исключительно выпуклые правильные многогранники.

Платоновы тела.

На рис. 2 изображены правильные многогранники. Простейшим из них является правильный тетраэдр, гранями которого служат четыре равносторонних треугольника и к каждой из вершин примыкают по три грани. Тетраэдру соответствует запись {3, 3}. Это не что иное, как частный случай треугольной пирамиды. Наиболее известен из правильных многогранников куб (иногда называемый правильным гексаэдром) – прямая квадратная призма, все шесть граней которой – квадраты. Так как к каждой вершине примыкают по 3 квадрата, куб обозначается {4, 3}. Если две конгруэнтные квадратные пирамиды с гранями, имеющими форму равносторонних треугольников, совместить основаниями, то получится многогранник, называемый правильным октаэдром. Он ограничен восемью равносторонними треугольниками, к каждой из вершин примыкают по четыре треугольника, и следовательно, ему соответствует запись {3, 4}. Правильный октаэдр можно рассматривать и как частный случай прямой правильной треугольной антипризмы. Рассмотрим теперь прямую правильную пятиугольную антипризму, грани которой имеют форму равносторонних треугольников, и две правильные пятиугольные пирамиды, основания которых конгруэнтны основанию антипризмы, а грани имеют форму равносторонних треугольников. Если эти пирамиды присоединить к антипризме, совместив их основания, то получится еще один правильный многогранник. Двадцать его граней имеют форму равносторонних треугольников, к каждой вершине примыкают по пять граней. Такой многогранник называется правильным икосаэдром и обозначается {3, 5}. Помимо четырех названных выше правильных многогранников, существует еще один – правильный додекаэдр, ограниченный двенадцатью пятиугольными гранями; к каждой его вершине примыкают по три грани, поэтому додекаэдр обозначается как {5, 3}.

Пять перечисленных выше правильных многогранников, часто называемых также «телами Платона », захватили воображение математиков, мистиков и философов древности более двух тысяч лет назад. Древние греки даже установили мистическое соответствие между тетраэдром, кубом, октаэдром и икосаэдром и четырьмя природными началами – огнем, землей, воздухом и водой. Что касается пятого правильного многогранника, додекаэдра, то они рассматривали его как форму Вселенной. Эти идеи не являются одним лишь достоянием прошлого. И сейчас, спустя два тысячелетия, многих привлекает лежащее в их основе эстетическое начало. О том, что они не утратили свою притягательность и поныне, весьма убедительно свидетельствует картина испанского художника Сальвадора Дали Тайная вечеря .

Древними греками исследовались также и многие геометрические свойства платоновых тел; с плодами их изысканий можно ознакомиться по 13-й книге Начал Евклида . Изучение платоновых тел и связанных с ними фигур продолжается и поныне. И хотя основными мотивами современных исследований служат красота и симметрия, они имеют также и некоторое научное значение, особенно в кристаллографии. Кристаллы поваренной соли, тиоантимонида натрия и хромовых квасцов встречаются в природе в виде куба, тетраэдра и октаэдра соответственно. Икосаэдр и додекаэдр среди кристаллических форм не встречаются, но их можно наблюдать среди форм микроскопических морских организмов, известных под названием радиолярий.

Число правильных многогранников.

Естественно спросить, существуют ли кроме платоновых тел другие правильные многогранники. Как показывают следующие простые соображения, ответ должен быть отрицательным. Пусть {p , q } – произвольный правильный многогранник. Так как его гранями служат правильные р -угольники, их внутренние углы, как нетрудно показать, равны (180 – 360/р ) или 180 (1 – 2/р ) градусам. Так как многогранник {p , q } выпуклый, сумма всех внутренних углов по граням, примыкающим к любой из его вершин, должна быть меньше 360 градусов. Но к каждой вершине примыкают q граней, поэтому должно выполняться неравенство

Нетрудно видеть, что p и q должны быть больше 2. Подставляя в (1) р = 3, мы обнаруживаем, что единственными допустимыми значениями q в этом случае являются 3, 4 и 5, т.е. получаем многогранники {3, 3}, {3, 4} и {3, 5}. При р = 4 единственным допустимым значением q является 3, т.е. многогранник {4, 3}, при р = 5 неравенству (1) также удовлетворяет только q = 3, т.е. многогранник {5, 3}. При p > 5 допустимых значений q не существует. Следовательно, других правильных многогранников, кроме тел Платона, не существует.

Все пять правильных многогранников перечислены в таблице, приведенной ниже. В трех последних столбцах указаны N 0 – число вершин, N 1 – число ребер и N 2 – число граней каждого многогранника.

К сожалению, приводимое во многих учебниках геометрии определение правильного многогранника неполно. Распространенная ошибка состоит в том, что в определении требуется лишь выполнение приведенного выше условия (i), но упускается из виду условие (ii). Между тем условие (ii) совершенно необходимо, в чем проще всего убедиться, рассмотрев выпуклый многогранник, удовлетворяющий условию (i), но не удовлетворяющий условию (ii). Простейший пример такого рода можно построить, отождествив грань правильного тетраэдра с гранью еще одного тетраэдра, конгруэнтного первому. В результате мы получим выпуклый многогранник, шестью гранями которого являются конгруэнтные равносторонние треугольники. Однако к одним вершинам примыкают три грани, а к другим – четыре, что нарушает условие (ii).

ПЯТЬ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
Название	Запись Шлефли	N 0 (число вершин)	N 1 (число ребер)	N 2 (число граней)
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр

Свойства правильных многогранников.

Двойственные многогранники.

Рассмотрим правильный многогранник {p , q } и его срединную сферу S . Средняя точка каждого ребра касается сферы. Заменяя каждое ребро отрезком перпендикулярной прямой, касательной к S в той же точке, мы получим N 1 ребер многогранника, двойственного многограннику {p , q }. Нетрудно показать, что гранями двойственного многогранника служат правильные q -угольники и что к каждой вершине примыкают р граней. Следовательно, многограннику {p , q } двойствен правильный многогранник {q , p }. Многограннику {3, 3} двойствен другой многогранник {3, 3}, конгруэнтный исходному (поэтому {3, 3} называется самодвойственным многогранником), многограннику {4, 3} двойствен многогранник {3, 4}, а многограннику {5, 3} – многогранник {3, 5}. На рис. 3 многогранники {4, 3} и {3, 4} показаны в положении двойственности друг другу. Кроме того, каждой вершине, каждому ребру и каждой грани многогранника {p , q } соответствует единственная грань, единственное ребро и единственная вершина двойственного многогранника {q , p }. Следовательно, если {p , q } имеет N 0 вершин, N 1 ребер и N 2 граней, то {q , p } имеет N 2 вершин, N 1 ребер и N 0 граней.

Так как каждая из N 2 граней правильного многогранника {p , q } ограничена р ребрами и каждое ребро является общим ровно для двух граней, то всего имеется pN 2 /2 ребер, поэтому N 1 = pN 2 /2. У двойственного многогранника {q , p } ребер также N 1 и N 0 граней, поэтому N 1 = qN 0 /2. Таким образом, числа N 0 , N 1 и N 2 для любого правильного многогранника {p , q } связаны соотношением

Симметрия.

Основной интерес к правильным многогранникам вызывает большое число симметрий, которыми они обладают. Под симметрией (или преобразованием симметрии) многогранника мы понимаем такое его движение как твердого тела в пространстве (например, поворот вокруг некоторой прямой, отражение относительно некоторой плоскости и т.д.), которое оставляет неизменными множества вершин, ребер и граней многогранника. Иначе говоря, под действием преобразования симметрии вершина, ребро или грань либо сохраняет свое исходное положение, либо переводится в исходное положение другой вершины, другого ребра или другой грани.

Существует одна симметрия, которая свойственна всем многогранникам. Речь идет о тождественном преобразовании, оставляющем любую точку в исходном положении. С менее тривиальным примером симметрии мы встречаемся в случае прямой правильной р -угольной призмы. Пусть l – прямая, соединяющая центры оснований. Поворот вокруг l на любое целое кратное угла 360/р градусов является симметрией. Пусть, далее, p – плоскость, проходящая посредине между основаниями параллельно им. Отражение относительно плоскости p (движение, переводящее любую точку P в точку P ў , такую, что p пересекает отрезок PP ў под прямым углом и делит его пополам) – еще одна симметрия. Комбинируя отражение относительно плоскости p с поворотом вокруг прямой l , мы получим еще одну симметрию.

Любую симметрию многогранника можно представить в виде произведения отражений. Под произведением нескольких движений многогранника как твердого тела здесь понимается выполнение отдельных движений в определенном заранее установленном порядке. Например, упоминавшийся выше поворот на угол 360/р градусов вокруг прямой l есть произведение отражений относительно любых двух плоскостей, содержащих l и образующих относительно друг друга угол в 180/р градусов. Симметрия, являющаяся произведением четного числа отражений, называется прямой, в противном случае – обратной. Таким образом, любой поворот вокруг прямой – прямая симметрия. Любое отражение есть обратная симметрия.

Рассмотрим подробнее симметрии тетраэдра, т.е. правильного многогранника {3, 3}. Любая прямая, проходящая через любую вершину и центр тетраэдра, проходит через центр противоположной грани. Поворот на 120 или 240 градусов вокруг этой прямой принадлежит к числу симметрий тетраэдра. Так как у тетраэдра 4 вершины (и 4 грани), то мы получим всего 8 прямых симметрий. Любая прямая, проходящая через центр и середину ребра тетраэдра проходит через середину противоположного ребра. Поворот на 180 градусов (полуоборот) вокруг такой прямой также является симметрией. Так как у тетраэдра 3 пары ребер, мы получаем еще 3 прямые симметрии. Следовательно, общее число прямых симметрий, включая тождественное преобразование, доходит до 12. Можно показать, что других прямых симметрий не существует и что имеется 12 обратных симметрий. Таким образом, тетраэдр допускает всего 24 симметрии. Для наглядности полезно построить картонную модель правильного тетраэдра и убедиться, что тетраэдр действительно обладает 24 симметриями. Развертки, которые можно вырезать из тонкого картона и, сложив, склеить из них пять правильных многогранников, приведены на рис. 4.

Прямые симметрии остальных правильных многогранников можно описать не по отдельности, а все вместе. Условимся понимать под {p , q } любой правильный многогранник, кроме {3, 3}. Прямая, проходящая через центр {p , q } и любую вершину, проходит через противоположную вершину, и любой поворот на целое кратное 360/q градусов вокруг этой прямой является симметрией. Следовательно, для каждой такой прямой существуют, включая тождественное преобразование, (q – 1) различных симметрий. Каждая такая прямая соединяет две из N 0 вершин; следовательно, всего таких прямых – N 0 /2, что дает (q – 1) > N 0 /2 симметрий. Кроме того, прямая, проходящая через центр многогранника {p , q } и центр любой грани, проходит через центр противоположной грани, и любой поворот вокруг такой прямой на целое кратное 360/р градусов является симметрией. Так как общее число таких линий равно N 2 /2, где N 2 – число граней многогранника {p , q }, мы получаем (p – 1) N 2 /2 различных симметрий, включая тождественное преобразование. Наконец, прямая, проходящая через центр и середину любого ребра многогранника {p , q }, проходит через середину противоположного ребра, и симметрией является полуоборот вокруг этой прямой. Поскольку имеется N 1 /2 таких прямых, где N 1 – число ребер многогранника {p , q }, мы получаем еще N 1 /2 симметрий. С учетом тождественного преобразования получаем

прямых симметрий. Других прямых симметрий нет, и имеется столько же обратных симметрий.

Хотя формула (3) была получена не для многогранника {3, 3}, нетрудно проверить, что она верна и для него. Таким образом, многогранник {3, 3} обладает 12 прямыми симметриями, многогранники {4, 3} и {3, 4} имеют по 24 симметрии, а многогранники {5, 3} и {3, 5} – по 60 симметрий.

Читатели, знакомые с абстрактной алгеброй, поймут, что симметрии многогранника {p , q } образуют группу относительно определенного выше «умножения». В этой группе прямые симметрии образуют подгруппу индекса 2, а обратные симметрии группу не образуют, так как нарушают свойство замкнутости и не содержат тождественного преобразования (единичного элемента группы). Обычно о группе прямых симметрий говорят как о группе многогранника, а полную группу симметрий называют его расширенной группой. Из рассмотренных выше свойств двойственных многогранников ясно, что любой правильный многогранник и двойственный ему многогранник имеют одну и ту же группу. Группа тетраэдра называется тетраэдрической группой, группа куба и октаэдра называется октаэдрической группой, а группа додекаэдра и икосаэдра – икосаэдрической группой. Они изоморфны знакопеременной группе А 4 из четырех символов, симметрической группе S 4 из четырех символов и знакопеременной группе А 5 из пяти символов соответственно .

ФОРМУЛА ЭЙЛЕРА

Рассматривая таблицу, можно заметить интересное соотношение между числом вершин N 0 , числом ребер N 1 и числом граней N 2 любого выпуклого правильного многогранника {p , q }. Речь идет о соотношении

Подставляя полученные выражения в формулы (3) и (4), получаем, что число прямых симметрий многогранника {p , q } равно

Это число можно записать также в одной из эквивалентных форм: qN 0 , 2N 1 или pN 2 .

Область применения формулы Эйлера.

Значимость формулы Эйлера усиливается тем, что она применима не только к платоновым телам, но и к любому многограннику, гомеоморфному сфере (см . ТОПОЛОГИЯ) . Это утверждение доказывается следующим образом.

Пусть P – любой многогранник, гомеоморфный сфере, с N 0 вершинами, N 1 ребрами и N 2 гранями; пусть c = N 0 – N 1 + N 2 – эйлерова характеристика многогранника P . Требуется доказать, что c = 2. Так как Р гомеоморфен сфере, мы можем удалить одну грань и превратить остальные в некоторую конфигурацию на плоскости (например, на рис. 5,а и 5,б вы видите призму, у которой удалена передняя плоскость). «Плоскостная конфигурация» представляет собой сеть точек и прямолинейных отрезков, называемых соответственно «вершинами» и «ребрами», при этом вершины служат концами ребер. Вершины и ребра рассматриваемой нами конфигурации мы считаем смещенными и деформированными вершинами и ребрами многогранника. Таким образом, эта конфигурация имеет N 0 вершин и N 1 ребер. Остальные N 2 – 1 граней многогранника деформируются в N 2 – 1 непересекающихся областей на плоскости, определяемой конфигурацией. Назовем эти области «гранями» конфигурации. Вершины, ребра и грани конфигурации и определяют эйлерову характеристику, которая в данном случае равна c – 1.

Теперь мы проведем сплющивание так, что если удаленная грань была р -угольником, то все N 2 – 1 граней конфигурации заполнят внутренность р -угольника. Пусть А – некоторая вершина внутри р -угольника. Предположим, что в А сходятся r ребер. Если удалить А и все r сходящихся в ней ребер, то число вершин уменьшится на 1, ребер – на r , граней – на r – 1 (см . рис. 5,б и 5,в ). У новой конфигурации Nў 0 = N 0 – 1 вершин, Nў 1 = N 1 – r ребер и Nў 2 = N 2 – 1 – (r – 1) граней; следовательно,

Таким образом, удаление одной внутренней вершины и сходящихся в ней ребер не меняет эйлеровой характеристики конфигурации. Поэтому, удалив все внутренние вершины и сходящиеся в них ребра, мы тем самым сведем конфигурацию к р -угольнику и его внутренности (рис. 5,г ). Но эйлерова характеристика останется по-прежнему равной c – 1, а так как конфигурация имеет р вершин, р ребер и 1 грань, мы получаем

Таким образом, c = 2, что и требовалось доказать.

Далее можно доказать, что если эйлерова характеристика многогранника равна 2, то многогранник гомеоморфен сфере. Иначе говоря, мы можем обобщить полученный выше результат, показав, что многогранник гомеоморфен сфере в том и только в том случае, если его эйлерова характеристика равна 2.

Обобщенная формула Эйлера.

Для классификации других многогранников используется обобщенная формула Эйлера. Если у некоторого многогранника 16 вершин, 32 ребра и 16 граней, то его эйлерова характеристика равна 16 – 32 + 16 = 0. Это позволяет утверждать, что данный многогранник принадлежит классу многогранников, гомеоморфных тору. Отличительной особенностью этого класса является эйлерова характеристика, равная нулю. Более общо, пусть Р – многогранник с N 0 вершинами, N 1 ребрами и N 2 гранями. Говорят, что данный многогранник гомеоморфен поверхности рода n в том и только в том случае, если

Наконец, следует заметить, что ситуация существенно усложняется, если смягчить прежнее ограничение, согласно которому никакие две грани многогранника не должны пересекаться. Например, появляется возможность существования двух негомеоморфных многогранников с одной и той же эйлеровой характеристикой. Их следует различать по другим топологическим свойствам.

Введение

Поверхность, составленную из многоугольников и ограничивающую некоторые геометрическое тело, называют многогранной поверхностью или многогранником.

Многогранником называется ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Многоугольники, которые ограничивают многогранник, называются гранями, линии пересечения граней называются ребрами.

Многогранники могут иметь разнообразное и очень сложное строение. Различные постройки, например строящиеся дома из кирпичей и бетонных блоков, представляют собой примеры многогранников. Другие примеры можно найти среди мебели, например стол. В химии форма молекул углеводорода представляет собой тетраэдр, правильного двадцатигранника, куб. В физики примером многогранников служат кристаллы.

С древнейших времен представления о красоте связывали с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей, которых поражала красота, совершенство, гармония этих фигур.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса. Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики - это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.

Пифагорейцы полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных тел:

§ Вселенная - додекаэдр

§ Земля - куб

§ Огонь - тетраэдр

§ Вода - икосаэдр

§ Воздух - октаэдр

Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться Платоновыми телами.

Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники. К каждой вершине правильного многогранника сходится одно и то же число рёбер. Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многоугольника равны. Платоновы тела - трехмерный аналог плоских правильных многоугольников.

Теория многогранников является современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления. Таким образом, данная тема является актуальной, а знания по данной проблематике – важными для современного общества.

Основная часть

Многогранникомназывается ограниченное тело, поверхность которого состоит из конечного числа многоугольников.

Приведем определение многогранника, равносильное первому определению многогранника.

Многогранник– это фигура, являющаяся объединением конечного числа тетраэдров, для которых выполнены следующие условия:

1) каждые два тетраэдра не имеют общих точек, либо имеют общую вершину, либо только общее ребро, либо целую общую грань;

2) от каждого тетраэдра к другому можно перейти по цепочке тетраэдра, в которой каждый последующий прилегает к предыдущему по целой грани.

Элементы многогранника

Грань многогранника – это некоторый многоугольник (многоугольником называется ограниченная замкнутая область, граница которой состоит из конечного числа отрезков).

Стороны граней называются ребрами многогранника, а вершины граней – вершинамимногогранника. К элементам многогранника, кроме его вершин, ребер и граней, относятся также плоские углы его граней и двугранные углы при его ребрах. Двугранный угол при ребре многогранника определяется его гранями, подходящими к этому ребру.

Классификация многогранников

Выпуклый многогранник - это многогранник, любые две точки которого соединимы в нем отрезком. Выпуклые многогранники обладают многими замечательными свойствами.

Теорема Эйлера. Для любого выпуклого многогранника В-Р+Г=2,

Где В – число его вершин, Р - число его ребер, Г - число его граней.

Теорема Коши. Два замкнутых выпуклых многогранника, одинаково составленные из соответственно равных граней равны.

Выпуклый многогранник считается правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходиться одно и то же число ребер.

Правильный многогранник

Многогранник называется правильным, если, во-первых, он выпуклый, во-вторых, все его грани - равные друг другу правильные многоугольники, в-третьих, в каждой его вершине сходятся одинаковое число граней, и, в-четвертых, все его двугранные углы равны.

Существует пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида (древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике). Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань. Гексаэдр (куб) имеет 6 граней, "гекса" - шесть; октаэдр - восьмигранник, "окто" - восемь; додекаэдр - двенадцатигранник, "додека" - двенадцать; икосаэдр имеет 20 граней, "икоси" - двадцать.

2.3. Типы правильных многогранников:

1) Правильный тетраэдр (составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольник. Следовательно, сумма плоских углов при каждой вершине равна 180 0);

2) Куб - параллелепипед, все грани которого – квадраты. Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 0 .

3) Правильный октаэдр или просто октаэдр – многогранник, у которого восемь правильных треугольных граней и в каждой вершине сходятся по четыре грани. Октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240 0 . Его можно построить, сложив основаниями две пирамиды, в основании которых квадраты, а боковые грани - правильные треугольники. Ребра октаэдра можно получить, соединяя центры соседних граней куба, если же соединить центры соседних граней правильного октаэдра, то получим ребра куба. Говорят, что куб и октаэдр двойственны друг другу.

4)Икосаэдр - составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 0 .

5) Додекаэдр - многогранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 0 .

Додекаэдр и икосаэдр тоже двойственны друг другу в том смысле, что, соединив отрезками центры соседних граней икосаэдра, мы получим додекаэдр, и наоборот.

Правильный тетраэдр двойственен сам себе.

При этом не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники при n ≥ 6.

Правильным многогранником называется многогранник, у которого все грани правильные равные многоугольники, и все двугранные углы равны. Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно-полуправильными многогранниками. Впервые многогранники такое типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда. Это усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр.

2.4. Полуправильные многогранники или Архимедовы тела - выпуклые многогранники, обладающие двумя свойствами:

1. Все грани являются правильными многоугольниками двух или более типов (если все грани - правильные многоугольники одного типа, это - правильный многогранник).

2. Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности все многогранные углы при вершинах конгруэнтны.

Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник. Иоганн Кеплерприсвоил этой фигуре имя «стелла октангула» - «восьмиугольная звезда». Она встречается и в природе: это так называемый двойной кристалл.

В определении правильного многогранника сознательно - в расчете на кажущуюся очевидность - не было подчеркнуто слово «выпуклый». А оно означает дополнительное требование: «и все грани, которого лежат по одну сторону от плоскости, проходящей через любую из них». Если же отказаться от такого ограничения, то к Платоновым телам, кроме «продолженного октаэдра», придется добавить еще четыре многогранника (их называют телами Кеплера - Пуансо), каждый из которых будет «почти правильным». Все они получаются «озвездыванием» Платонова тела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются.

Если же продлить все грани октаэдра до пересечения их друг с другом, то получится фигура, что возникает при взаимопроникновении двух тетраэдров - «стелла октангула», которая называется «продолженным октаэдром».

Икосаэдр и додекаэдр дарят миру сразу четыре «почти правильных многогранника». Один из них - малый звездчатый додекаэдр, полученный впервые Иоганном Кеплером.

Столетиями математики не признавали за всякого рода звездами права называться многоугольниками из-за того, что стороны их пересекаются. Людвиг Шлефли не изгонял геометрическое тело из семейства многогранников только за то, что его грани самопересекаются, тем не менее, оставался непреклонным, как только речь заходила про малый звездчатый додекаэдр. Довод его был прост и весом: это кеплеровское животное не подчиняется формуле Эйлера! Его колючки образованы двенадцатью гранями, тридцатью ребрами и двенадцатью вершинами, и, следовательно, В+Г-Р вовсе не равняется двойке.

Шлефли был и прав, и не прав. Конечно же, геометрический ежик не настолько уж колюч, чтобы восстать против непогрешимой формулы. Надо только не считать, что он образован двенадцатью пересекающимися звездчатыми гранями, а взглянуть на него как на простое, честное геометрическое тело, составленное из 60 треугольников, имеющее 90 ребер и 32 вершины.

Тогда В+Г-Р=32+60-90 равно, как и положено, 2. Но зато тогда к этому многограннику неприменимо слово «правильный» - ведь грани его теперь не равносторонние, а всего лишь равнобедренные треугольники. Кеплер не додумался, что у полученной им фигуры есть двойник.

Многогранник, который называется «большой додекаэдр» - построил французский геометр Луи Пуансо спустя двести лет после кеплеровских звездчатых фигур.

Большой икосаэдрбыл впервые описан Луи Пуансо в 1809 году. И опять Кеплер, увидев большой звездчатый додекаэдр, честь открытия второй фигуры оставил Луи Пуансо. Эти фигуры также наполовину подчиняются формуле Эйлера.

Практическое применение

Многогранники в природе

Правильные многогранники – самые выгодные фигуры, поэтому они широко распространены в природе. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба. При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму правильного октаэдра. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана. Кристаллы этого химического вещества имеют форму додекаэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора.

Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Оно больше похоже на звёздчатый многогранник.

Также мы можем наблюдать многогранники в виде цветов. Ярким примером могут служить кактусы.

Похожая информация.

Многогранники не только занимают видное место в геометрии, но и встречаются в повседневной жизни каждого человека. Не говоря уже об искусственно созданных предметах обихода в виде различных многоугольников, начиная со спичечного коробка и заканчивая архитектурными элементами, в природе также встречаются кристаллы в форме куба (соль), призмы (хрусталь), пирамиды (шеелит), октаэдра (алмаз) и т. д.

Понятие многогранника, виды многогранников в геометрии

Геометрия как наука содержит раздел стереометрию, изучающую характеристики и свойства объёмных тела, стороны которых в трёхмерном пространстве образованы ограниченными плоскостями (гранями), носят название "многогранники". Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.

Тем не менее у всех многогранников есть общие свойства:

Все они имеют 3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.

Многогранники можно условно разделить на:

Виды выпуклых многогранников, состоящих из следующих классов: обычные или классические (призма, пирамида, параллелепипед), правильные (также называемые Платоновыми телами), полуправильные (второе название - Архимедовы тела).
Невыпуклые многогранники (звёздчатые).

Призма и её свойства

Стереометрия как раздел геометрии изучает свойства трёхмерных фигур, виды многогранников (призма в их числе). Призмой называют геометрическое тело, которое имеет обязательно две совершенно одинаковые грани (их также называют основаниями), лежащие в параллельных плоскостях, и n-ое число боковых граней в виде параллелограммов. В свою очередь, призма имеет также несколько разновидностей, в числе которых такие виды многогранников, как:

Параллелепипед - образуется, если в основании лежит параллелограмм - многоугольник с 2 парами равных противоположных углов и двумя парами конгруэнтных противоположных сторон.
имеет перпендикулярные к основанию рёбра.
характеризуется наличием непрямых углов (отличных от 90) между гранями и основанием.
Правильная призма характеризуется основаниями в виде с равными боковыми гранями.

Основные свойства призмы:

Конгруэнтные основания.
Все рёбра призмы равны и параллельны по отношению друг к другу.
Все боковые грани имеют форму параллелограмма.

Пирамида

Пирамидой называют геометрическое тело, которое состоит из одного основания и из n-го числа треугольных граней, соединяющихся в одной точке - вершине. Следует отметить, что если боковые грани пирамиды представлены обязательно треугольниками, то в основании может быть как треугольный многоугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании. Например, если в основании пирамиды лежит треугольник - это , четырёхугольник - четырёхугольная, и т. д.

Пирамиды - это конусоподобные многогранники. Виды многогранников этой группы, кроме вышеперечисленных, включают также следующих представителей:

имеет в основании правильный многоугольник, и высота ее проектируется в центр окружности, вписанной в основание или описанной вокруг него.
Прямоугольная пирамида образуется тогда, когда одно из боковых рёбер пересекается с основанием под прямым углом. В таком случае это ребро справедливо также назвать высотой пирамиды.

Свойства пирамиды:

В случае если все боковые рёбра пирамиды конгруэнтны (одинаковой высоты), то все они пересекаются с основанием под одним углом, а вокруг основания можно прочертить окружность с центром, совпадающим с проекцией вершины пирамиды.
Если в основании пирамиды лежит правильный многоугольник, то все боковые рёбра конгруэнтны, а грани являются равнобедренными треугольниками.

Правильный многогранник: виды и свойства многогранников

В стереометрии особое место занимают геометрические тела с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:

Тетраэдр.
Гексаэдр.
Октаэдр.
Додекаэдр.
Икосаэдр.

Своим названием правильные многогранники обязаны древнегреческому философу Платону, описавшему эти геометрические тела в своих трудах и связавшему их с природными стихиями: земли, воды, огня, воздуха. Пятой фигуре присуждали сходство со строением Вселенной. По его мнению, атомы природных стихий по форме напоминают виды правильных многогранников. Благодаря своему самому захватывающему свойству - симметричности, эти геометрические тела представляли большой интерес не только для древних математиков и философов, но и для архитекторов, художников и скульпторов всех времён. Наличие всего лишь 5 видов многогранников с абсолютной симметрией считалось фундаментальной находкой, им даже присуждали связь с божественным началом.

Гексаэдр и его свойства

В форме шестигранника преемники Платона предполагали сходство со строением атомов земли. Конечно же, в настоящее время эта гипотеза полностью опровергнута, что, однако, не мешает фигурам и в современности привлекать умы известных деятелей своей эстетичностью.

В геометрии гексаэдр, он же куб, считается частным случаем параллелепипеда, который, в свою очередь, является разновидностью призмы. Соответственно и свойства куба связаны со с той лишь разницей, что все грани и углы куба равны между собой. Из этого вытекают следующие свойства:

Все рёбра куба конгруэнтны и лежат в параллельных плоскостях по отношению друг к другу.
Все грани - конгруэнтные квадраты (всего в кубе их 6), любой из которых может быть принят за основание.
Все межгранные углы равны 90.
Из каждой вершины исходит равное количество рёбер, а именно 3.
Куб имеет 9 которые все пересекаются в точке пересечения диагоналей гексаэдра, именуемой центром симметрии.

Тетраэдр

Тетраэдр - это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.

Свойства правильного тетраэдра:

Все грани тетраэда - это из чего следует, что все грани четырёхгранника конгруэнтны.
Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.

Октаэдр и его свойства

Описывая виды правильных многогранников, нельзя не отметить такой объект, как октаэдр, который визуально можно представить в виде двух склеенных основаниями четырёхугольных правильных пирамид.

Свойства октаэдра:

Само название геометрического тела подсказывает количество его граней. Восьмигранник состоит из 8 конгруэнтных равносторонних треугольников, в каждой из вершин которого сходится равное количество граней, а именно 4.
Так как все грани октаэдра равны, равны и его межгранные углы, каждый из которых равняется 60, а сумма плоских углов любой из вершин составляет, таким образом, 240.

Додекаэдр

Если представить, что все грани геометрического тела представляют собой правильный пятиугольник, то получится додекаэдр - фигура из 12 многоугольников.

Свойства додекаэдра:

В каждой вершине пересекаются по три грани.
Все грани равны и имеют одинаковую длину рёбер, а также равную площадь.
У додекаэдра 15 осей и плоскостей симметрии, причём любая из них проходит через вершину грани и середину противоположного ей ребра.

Икосаэдр

Не менее интересная, чем додекаэдр, фигура икосаэдр представляет собой объёмное геометрическое тело с 20 равными гранями. Среди свойств правильного двадцатигранника можно отметить следующие:

Все грани икосаэдра - равнобедренные треугольники.
В каждой вершине многогранника сходится пять граней, и сумма смежных углов вершины составляет 300.
Икосаэдр имеет так же, как и додекаэдр, 15 осей и плоскостей симметрии, проходящих через середины противоположных граней.

Полуправильные многоугольники

Кроме Платоновых тел, в группу выпуклых многогранников входят также Архимедовы тела, которые представляют собой усечённые правильные многогранники. Виды многогранников данной группы обладают следующими свойствами:

Геометрические тела имеют попарно равные грани нескольких типов, например, усечённый тетраэдр имеет так же, как и правильный тетраэдр, 8 граней, но в случае Архимедова тела 4 грани будут треугольной формы и 4 - шестиугольной.
Все углы одной вершины конгруэнтны.

Звёздчатые многогранники

Представители необъёмных видов геометрических тел - звёздчатые многогранники, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.

Таким образом, известны такие звёздчатые многогранники, как: звёздчатые формы октаэдра, додекаэдра, икосаэдра, кубооктаэдра, икосододекаэдра.