Một khối đa diện gồm một đa giác gọi là đáy. Khái niệm về khối đa diện

Đây là một vật thể có bề mặt bao gồm một số lượng hữu hạn các đa giác phẳng. Khối đa diện được gọi là lồi, nếu nó nằm trên một cạnh của mặt phẳng của mỗi đa giác phẳng trên bề mặt của nó. Phần chung của mặt phẳng đó và bề mặt của đa giác lồi được gọi là bờ rìa.
Hình dưới đây thể hiện một khối đa diện không lồi ở bên trái; trong hình bên phải - lồi.

Các mặt của khối đa diện lồi là các đa giác lồi phẳng. Các cạnh của khuôn mặt được gọi là các cạnh của khối đa diện, và các đỉnh của các mặt là các đỉnh của khối đa diện.

lăng kính

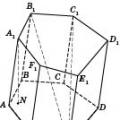
lăng kínhđược gọi là một khối đa diện, bao gồm hai đa giác phẳng nằm trong các mặt phẳng khác nhau và được kết hợp bằng phép dịch song song và tất cả các đoạn nối các điểm tương ứng của các đa giác này (xem hình). Đa giác được gọi cơ sở lăng kính và các đoạn nối các đỉnh tương ứng là các cạnh bên của lăng kính.

Các chỉ định: .
Bề mặt bên của lăng kính bao gồm các hình bình hành. Mỗi trong số chúng có hai mặt, là các mặt tương ứng của đế và hai mặt còn lại là các gân bên liền kề. Các đáy của lăng kính bằng nhau và nằm trong các mặt phẳng song song. Các cạnh bên của lăng kính song song và bằng nhau. Chiều cao lăng kínhđược gọi là khoảng cách giữa các mặt phẳng đáy của nó.
Đoạn thẳng nối hai đỉnh của lăng kính không thuộc cùng một mặt được gọi là lăng kính chéo. (Hình vẽ cho thấy chiều cao và đường chéo.)
Mặt cắt chéo- đây là những phần của lăng kính bởi các mặt phẳng đi qua hai cạnh bên không thuộc cùng một mặt (xem hình ảnh).

Lăng kính được gọi là thẳng, nếu các cạnh bên của nó vuông góc với các đáy. Ngược lại lăng kính được gọi là nghiêng.
Các mặt bên của hình lăng trụ thẳng là hình chữ nhật, chiều cao của hình lăng trụ thẳng bằng cạnh bên, các đường chéo là hình chữ nhật.
Bề mặt bên của lăng kính bằng tổng diện tích các mặt bên. Bề mặt lăng kính đầy đủ bằng tổng diện tích xung quanh và diện tích các đáy.
Định lý 1. Bề mặt bên của một lăng trụ thẳng bằng tích của chu vi đáy và chiều cao, tức là chiều dài của cạnh bên.
Tiết diện vuông góc của lăng kính chúng ta sẽ gọi tiết diện này là mặt phẳng vuông góc với cạnh bên của lăng kính (có nghĩa là mặt phẳng này vuông góc với tất cả các cạnh bên của lăng kính).
Định lý 2. Bề mặt bên của lăng trụ nghiêng bằng tích của chiều dài cạnh bên và chu vi tiết diện vuông góc.
Hình vẽ cho thấy một phần vuông góc.
S b = H ⋅ P nền tảng;
S n = S b + 2 S nền tảng
S b = tôi ⋅ P ter;
S n = S b + 2 S nền tảng

Rõ ràng định lý này cũng đúng trong trường hợp lăng trụ thẳng, vì khi đó tiết diện vuông góc sẽ là tiết diện bởi một mặt phẳng song song với các mặt phẳng đáy của lăng trụ.
Xin lưu ý: nếu một đa giác nhất định là phần vuông góc của lăng kính thì các góc trong của nó là các góc tuyến tính của các góc nhị diện giữa các mặt bên tương ứng.
Trong trường hợp lăng kính thẳng, các góc tuyến tính của các góc nhị diện giữa các mặt bên trực tiếp là các góc của đáy.
Ví dụ
Hình vẽ cho thấy một lăng kính thẳng.

- góc tuyến tính của góc lưỡng diện giữa các mặt và .
Lăng kính được gọi là Chính xác, Nếu như:
nó dựa trên một đa giác đều;
lăng kính thẳng.

song song

Hình bình hành là một hình lăng trụ có hình bình hành ở đáy.
Tất cả các mặt của hình bình hành đều là hình bình hành.
Các mặt của hình bình hành không có đỉnh chung được gọi là đối diện.
Định lý 1. Các mặt đối diện của hình bình hành thì song song và bằng nhau.
Một đường ống song song vẫn là một đường ống song song trong mọi trường hợp khi chúng ta coi bất kỳ mặt nào của nó làm cơ sở (xem hình).
Định lý 2. Các đường chéo của một hình bình hành cắt nhau tại một điểm và được chia đôi cho giao điểm.
Từ đó suy ra rằng giao điểm của các đường chéo của một hình bình hành là tâm đối xứng của nó.
Xin lưu ý: một hình bình hành bên phải có bốn đường chéo bằng nhau.
Trên hình ảnh; .
Điều này suy ra từ tính chất của các vật nghiêng, vì vậy - vuông góc với mặt phẳng đáy A B C D.

Nếu hai đường chéo của một hình bình hành vuông xuất hiện từ các đỉnh liền kề thì đường chéo lớn hơn là đường chéo chiếu vào đường chéo lớn của đáy, tức là đường chéo của hình bình hành nằm đối diện với góc tù. Do đó, nếu trong hình trên chúng ta xét góc ABC ngu ngốc, chúng ta sẽ hiểu được, .
Hình bình hành bên phải có đáy là hình chữ nhật được gọi là hình chữ nhật song song(xem hình).

Tất cả các mặt của hình bình hành hình chữ nhật đều là hình chữ nhật có thể chia thành ba cặp mặt bằng nhau. Một mặt tùy ý của hình song song hình chữ nhật có thể được coi là cơ sở của nó. Xét rằng trong thiết kế song song, một hình bình hành tùy ý có thể được biểu diễn bằng một hình bình hành tùy ý, hình ảnh của một hình bình hành hình chữ nhật không khác gì hình ảnh của bất kỳ hình bình hành bên phải nào.
Độ dài các cạnh không song song được gọi là kích thước tuyến tính(số đo) của hình chữ nhật song song.
Định lý 3. Trong một hình bình hành hình chữ nhật, mọi đường chéo đều bằng nhau. Bình phương của một đường chéo bằng tổng các bình phương ba chiều của nó.
Mọi góc nhị diện của hình bình hành đều là góc vuông.
Một hình bình hành hình chữ nhật có ba cặp đường chéo bằng nhau. Mỗi phần này là một hình chữ nhật (xem hình ảnh).

Mỗi cặp phần cắt nhau dọc theo một đường thẳng đi qua giao điểm của các đường chéo của các mặt đối diện. Các đoạn giữa các điểm này song song và bằng một trong các cạnh của hình chữ nhật song song.
Một tam giác vuông, được hình thành bởi đường chéo của hình chữ nhật song song, đường chéo của mặt bên và cạnh của đáy (xem hình). Ví dụ, .

Một hình song song hình chữ nhật có tâm đối xứng - đây là điểm giao nhau của các đường chéo của nó.
Nó cũng có ba mặt phẳng đối xứng chạy qua tâm đối xứng song song với các mặt.
Một hình chữ nhật có tất cả các cạnh bằng nhau được gọi là khối lập phương.
Mặt phẳng của bất kỳ phần đường chéo nào của hình lập phương là mặt phẳng đối xứng của nó. Như vậy, khối lập phương có chín mặt phẳng đối xứng.
Trong hình, chúng ta xét vị trí tương đối của một số phần tử của hình bình hành bên phải:

- góc giữa đường chéo của mặt bên và mặt phẳng đáy ( - vuông góc, - nghiêng, đĩa CD- phép chiếu).
- góc giữa đường chéo của hình bình hành bên phải và mặt phẳng đáy ( - vuông góc, - nghiêng, AC- phép chiếu).
- góc nghiêng của đường chéo với mặt bên ( QUẢNG CÁO- vuông góc, - xiên, - hình chiếu).
Giả sử là một hình bình hành bên phải (xem hình), trong đó A B C D- hình thoi Chúng ta hãy vẽ mặt cắt của nó bằng một mặt phẳng đi qua đường chéo của đáy BD và đỉnh cao.

Trong mặt cắt ngang, chúng ta thu được một tam giác cân.
- góc tuyến tính của góc nhị diện giữa các mặt phẳng của đáy và mặt cắt. theo tính chất các đường chéo của hình thoi, - vuông góc, - xiên, CO- phép chiếu. Theo định lý ba đường vuông góc: .

Kim tự tháp

Kim tự thápđược gọi là khối đa diện bao gồm một đa giác phẳng - đáy của hình chóp, một điểm không nằm trong mặt phẳng của đáy - đỉnh của hình chóp và tất cả các đoạn nối đỉnh của hình chóp với các điểm của đáy. Các đoạn nối đỉnh của hình chóp với các đỉnh của đáy được gọi là xương sườn bên.
chiều cao kim tự tháp- một đường vuông góc hạ từ đỉnh kim tự tháp xuống mặt phẳng đáy.
Kim tự tháp được gọi là N-than đá, nếu cơ sở của nó là N-gon. Kim tự tháp tam giác còn được gọi là tứ diện. Mặt bên của kim tự tháp- Tam giác. Một trong các đỉnh của nó là đỉnh của kim tự tháp, và cạnh đối diện là cạnh đáy của kim tự tháp.
Trên hình ảnh VÌ THẾ- chiều cao của kim tự tháp. Sau đó - góc giữa cạnh bên và mặt phẳng đáy ( VÌ THẾ- vuông góc, SA- nghiêng, viêm khớp- phép chiếu).

Tính từ đáy chiều cao của kim tự tháp (điểm TRONG) vẽ một đường vuông góc với cạnh của đế (ví dụ: AE). Đáy của đường vuông góc này (điểm F) kết nối với đỉnh của kim tự tháp (điểm S). Theo định lý ba đường vuông góc: . ( VÌ THẾ- vuông góc, SP- nghiêng, CỦA- phép chiếu, do xây dựng.) Do đó, - góc tuyến tính của góc nhị diện giữa mặt phẳng của mặt bên ASE và mặt phẳng của đáy.
Để giải các bài toán về kim tự tháp, điều rất quan trọng là phải tìm ra đâu là đáy của chiều cao của nó.
1. Nếu đáp ứng ít nhất một trong các điều kiện sau:
tất cả các cạnh bên của kim tự tháp đều bằng nhau;
tất cả các gân bên đều nghiêng so với mặt phẳng đáy một góc;
tất cả các gân bên tạo thành các góc bằng nhau với chiều cao của kim tự tháp;
tất cả các cạnh bên cách đều đáy có chiều cao thì đáy có chiều cao của hình chóp là tâm của đường tròn ngoại tiếp đáy của hình chóp.
sườn bên tôi, chiều cao H và bán kính R ngoại tiếp đáy hình tròn tạo thành một tam giác vuông:

Trong trường hợp này, bề mặt bên có thể được tìm thấy bằng công thức, trong đó tôi- chiều dài cạnh bên, , ... - góc phẳng ở đỉnh.
2. Nếu đáp ứng ít nhất một trong các điều kiện sau:
tất cả các mặt bên đều nghiêng so với mặt phẳng đáy một góc;
tất cả các mặt bên có cùng chiều cao;
chiều cao của các mặt bên tạo thành các góc bằng chiều cao của hình chóp;
các mặt bên cách đều đáy của chiều cao thì đáy của chiều cao nằm ở tâm của hình tròn nội tiếp ở đáy hình chóp.
Trên hình ảnh - hình chữ nhật, - bán kính của hình tròn nội tiếp trong ABCDEF;

- chiều cao của kim tự tháp, SP- chiều cao của mặt bên;
- góc tuyến tính của góc nhị diện giữa mặt bên và mặt phẳng đáy;
VỀ- tâm của đường tròn nội tiếp ở đáy, tức là giao điểm của các đường phân giác ABCDEF.
Trong trường hợp này .
3. Nếu cạnh bên vuông góc với mặt phẳng đế thì cạnh này chính là chiều cao của hình chóp (xem hình).

Trong trường hợp này Và - góc nghiêng của các xương sườn bên SВ Và SC tương ứng với mặt phẳng đáy. là góc tuyến tính của góc nhị diện giữa các mặt bên S.A.C. Và S.B.A..

4. Nếu mặt bên vuông góc với mặt phẳng đáy (xem hình) thì chiều cao của hình chóp sẽ bằng chiều cao của mặt này (theo định lý “Nếu một đường thẳng nằm trên một trong hai mặt phẳng vuông góc thì vuông góc với giao tuyến của chúng thì vuông góc với mặt phẳng thứ hai”).
5. Nếu hai mặt bên vuông góc với mặt phẳng đáy thì chiều cao của hình chóp là cạnh chung của chúng.

Khoảng cách từ chân đế của chiều cao của kim tự tháp

Khoảng cách từ đáy của hình chóp đến cạnh bên là đường vuông góc hạ từ một điểm VỀ trên cạnh này (xem hình). Xin lưu ý: , nhưng trong hình không được thẳng: các góc không được bảo toàn trong quá trình thiết kế song song.
CỦA- khoảng cách từ chân đế đến cạnh bên S.E.;
TRÊN- khoảng cách từ chân đế đến cạnh bên A.S.B.(Xem khoảng cách này chi tiết hơn bên dưới).

, góc giữa cạnh ở đâu S.E. và mặt phẳng của đáy.

Khoảng cách từ chân đế của chiều cao đến cạnh bên

Giả sử , thì theo định lý ba đường vuông góc. Kể từ đây, AB vuông góc với mặt phẳng SOK. Do đó, nếu , thì TRÊN vuông góc với mặt phẳng A.S.B..
.
Kim tự tháp được gọi là Chính xác, nếu đáy của nó là một đa giác đều và đáy có chiều cao trùng với tâm của đa giác. Trục của một hình chóp đều là đường thẳng chứa chiều cao của nó. Các cạnh bên của hình chóp đều bằng nhau, các mặt bên là các tam giác cân bằng nhau. Chiều cao của mặt bên vẽ từ đỉnh kim tự tháp được gọi là huyền thoại. Nó là đường phân giác và đường trung bình của mặt bên, vì nó là tam giác cân.
Định lý. Bề mặt bên của một hình chóp đều bằng tích của chu vi đáy và đường trung đoạn.
; ,
Ở đâu R- chu vi cơ sở, MỘT- mặt đế, tôi- chiều dài của trung đoạn.
Kim tự tháp tam giác đều
Đáy của một hình chóp tam giác đều là một tam giác đều, được biểu thị bằng một tam giác tùy ý (xem hình).

Tâm là giao điểm của các đường phân giác của nó, vừa là đường cao vừa là đường trung tuyến. Trong thiết kế song song, các dải phân cách được mô tả là các dải phân cách. Do đó, chúng ta dựng hai đường trung tuyến của đáy. Điểm giao nhau của chúng là đáy của chiều cao của kim tự tháp. Chúng tôi mô tả chiều cao, sau đó nối đỉnh của kim tự tháp với các đỉnh của đế. Chúng tôi nhận được các xương sườn bên.
Trong hình: - góc nghiêng của gân bên với mặt phẳng của đế (như nhau đối với tất cả các gân); - góc nghiêng của mặt bên với mặt phẳng của đế (như nhau đối với tất cả các mặt).
Cho phép .
Sau đó ; ; ;
; ; .
Kể từ đây, .
; .
Mặt cắt trục A.S.D. là mặt phẳng đối xứng của hình chóp tam giác đều.
Mặt phẳng này vuông góc với mặt phẳng đáy và mặt phẳng cạnh BSC.
Điều thú vị cần lưu ý là các cạnh giao nhau của kim tự tháp ( SA Và BC, S.B. Và AC., S.C. Và AB) vuông góc. Nếu , thì TRÊN là khoảng cách từ chân đế của chiều cao không chỉ đến lỗ thông mà còn đến mặt bên BSC.
.
Kim tự tháp tứ giác đều
Dưới đáy của một kim tự tháp tứ giác đều có một hình vuông, được mô tả dưới dạng hình bình hành tùy ý. Tâm của nó là giao điểm của các đường chéo. Điểm này là đáy của chiều cao của kim tự tháp.
Hãy để cạnh của hình vuông MỘT(xem hình).
Sau đó ;
;
;
;
.

Xin lưu ý: , , tức là .
Với thiết kế song song, tính song song được duy trì.
; .
Khoảng cách từ chân đế đến cạnh bên:
; .

Kim tự tháp lục giác đều
Cơ sở của hình chóp lục giác đều là hình lục giác đều (xem hình). Tâm của nó là giao điểm của các đường chéo. Điểm này là đáy của chiều cao của kim tự tháp.
Sau đó ;
Hãy để cạnh của một hình lục giác đều MỘT.
;
;

.
; .

Kim tự tháp cắt ngắn
Cắt theo kim tự thápđược gọi là khối đa diện sẽ còn lại nếu một hình chóp có cùng một đỉnh được ngăn cách với hình chóp bằng một mặt phẳng song song với đáy.
Định lý. Một mặt phẳng song song và cắt đáy của một kim tự tháp sẽ cắt một kim tự tháp tương tự.
Xin lưu ý: để mô tả chính xác kim tự tháp đã cắt, bạn phải bắt đầu bằng việc mô tả kim tự tháp đầy đủ ban đầu (xem hình).

Các đáy của một hình chóp cụt là các đa giác giống nhau. Các mặt bên có hình thang. - chiều cao của hình chóp cụt, - chiều cao của mặt bên, - góc nghiêng của cạnh bên với mặt phẳng của đế (bất kỳ), - góc nghiêng của mặt bên với mặt phẳng bên dưới căn cứ.
Kim tự tháp cắt ngắn thông thường- đây là một kim tự tháp cắt ngắn được lấy từ một kim tự tháp thông thường.
Các gân bên của nó bằng nhau và nghiêng với mặt phẳng của đế một góc như nhau. Các mặt bên của nó bằng hình thang nằm ngang và cùng nghiêng với mặt phẳng của đáy dưới một góc. Chiều cao của các mặt bên của kim tự tháp được gọi là lời châm ngôn.
Bề mặt bên của một hình chóp cụt đều bằng tích của một nửa tổng chu vi của các đáy và trung đoạn.
, Ở đâu P n và P- chu vi của các căn cứ tương ứng, tôi- lời nguyền.
Các hình ảnh thể hiện những hình vẽ có thể rất hữu ích để xem xét khi giải các bài toán liên quan đến hình chóp bị cắt.
;
.

;

- hình thang chữ nhật.
- chiều cao của kim tự tháp bị cắt cụt.
- chiều cao cạnh bên.

Trong trường hợp hình chóp cụt là đều, các đoạn OD và là bán kính của đường tròn ngoại tiếp, và CỦA và - bán kính của đường tròn nội tiếp tương ứng với đáy dưới và đáy trên.

khối đa diện đều

Một khối đa diện lồi được gọi là Chính xác, nếu các mặt của nó là các khối đa diện đều có cùng số cạnh và cùng số cạnh trùng nhau tại mỗi đỉnh của khối đa diện.
Có năm loại khối đa diện lồi đều: tứ diện đều, khối lập phương, bát diện, khối mười hai mặt, khối hai mươi mặt.
1. Tứ diện đều có các mặt là hình tam giác đều; Mỗi đỉnh có ba cạnh trùng nhau. Tứ diện là một hình chóp tam giác có tất cả các cạnh bằng nhau.
2. Tất cả các mặt của hình lập phương đều là hình vuông; Mỗi đỉnh có ba cạnh trùng nhau. Hình lập phương là hình chữ nhật có các cạnh bằng nhau.
3. Các mặt của hình bát diện là những hình tam giác đều. Mỗi đỉnh của nó có bốn cạnh trùng nhau.
4. Các mặt của khối mười hai mặt đều là các hình ngũ giác đều. Tại mỗi đỉnh của nó có ba cạnh trùng nhau.
5. Các mặt của khối hai mươi mặt đều chứa các hình tam giác đều. Tại mỗi đỉnh của nó có năm cạnh trùng nhau.
Các hình vẽ cho thấy các ví dụ về khối đa diện đều có tên.

Mặc dù phép đo lập thể chỉ được học ở trường trung học, nhưng mọi học sinh đều quen thuộc với hình lập phương, hình chóp đều và các khối đa diện đơn giản khác. Chủ đề “Khối đa diện” có những ứng dụng tươi sáng, bao gồm cả trong hội họa và kiến trúc. Ngoài ra, theo cách diễn đạt tượng hình của Viện sĩ Alexandrov, nó là sự kết hợp giữa “băng và lửa”, tức là trí tưởng tượng sống động và logic chặt chẽ. Nhưng trong khóa học về hình học lập thể, rất ít thời gian được dành cho các khối đa diện đều. Nhưng đối với nhiều người, các khối đa diện đều rất được quan tâm nhưng lại không có cơ hội tìm hiểu thêm về chúng trên lớp. Đó là lý do tại sao tôi quyết định nói về tất cả các khối đa diện đều có nhiều hình dạng khác nhau và những đặc tính thú vị của chúng.

Cấu trúc của khối đa diện đều rất thuận tiện cho việc nghiên cứu nhiều phép biến đổi của khối đa diện thành chính nó (xoay, đối xứng, v.v.). Các nhóm biến đổi thu được (chúng được gọi là nhóm đối xứng) hóa ra rất thú vị theo quan điểm của lý thuyết nhóm hữu hạn. Sự đối xứng tương tự giúp tạo ra một loạt câu đố dưới dạng khối đa diện đều, bắt đầu bằng “khối Rubik” và “kim tự tháp Moldavian”.

Để biên soạn phần tóm tắt, chúng tôi đã sử dụng tạp chí khoa học và toán học nổi tiếng “Lượng tử”, từ đó lấy thông tin về thế nào là một khối đa diện đều, về số lượng của chúng, về cấu trúc của tất cả các khối đa diện đều và mô tả về tất cả các phép quay mà khối đa diện đó thực hiện. được kết hợp với vị trí ban đầu của nó. Từ tờ báo "Toán học", tôi đã nhận được những thông tin thú vị về các khối đa diện đều có hình sao, tính chất, khám phá và ứng dụng của chúng.

Bây giờ bạn có cơ hội lao vào thế giới của những điều đúng đắn và tráng lệ, vào thế giới của những điều đẹp đẽ và phi thường, làm say đắm đôi mắt chúng ta.

1. Khối đa diện đều

1.1 Định nghĩa khối đa diện đều.

Một khối đa diện lồi được gọi là đều nếu các mặt của nó là các khối đa diện đều bằng nhau và tất cả các góc đa diện đều bằng nhau.

Chúng ta hãy xem xét các khối đa diện đều có thể và trước hết là những khối có mặt là hình tam giác đều. Khối đa diện đều đơn giản nhất là hình chóp tam giác, các mặt của nó là các hình tam giác đều. Ba mặt gặp nhau ở mỗi đỉnh của nó. Chỉ có bốn mặt, khối đa diện này còn được gọi là tứ diện đều, hay đơn giản là tứ diện, dịch từ tiếng Hy Lạp có nghĩa là tứ diện.

Một khối đa diện có các mặt là các hình tam giác đều và có bốn mặt gặp nhau ở mỗi đỉnh, bề mặt của nó gồm 8 hình tam giác đều nên gọi là khối bát diện.

Một khối đa diện trong đó có năm hình tam giác đều gặp nhau ở mỗi đỉnh. Bề mặt của nó bao gồm hai mươi hình tam giác đều, đó là lý do tại sao nó được gọi là khối hai mươi mặt.

Lưu ý rằng vì có hơn năm hình tam giác đều không thể gặp nhau tại các đỉnh của một khối đa diện lồi nên không có đa giác đều nào khác có các mặt là hình tam giác đều.

Tương tự, vì chỉ có ba hình vuông có thể hội tụ tại các đỉnh của một khối đa diện lồi, nên ngoài khối lập phương, không có khối đa diện đều nào khác có các mặt là hình vuông. Hình lập phương có sáu mặt nên còn được gọi là hình lục giác.

Một khối đa diện có các mặt là ngũ giác đều và có ba mặt gặp nhau ở mỗi đỉnh. Bề mặt của nó bao gồm mười hai hình ngũ giác đều, đó là lý do tại sao nó được gọi là khối mười hai mặt.

Từ định nghĩa của một khối đa diện đều, ta suy ra rằng một khối đa diện đều “đối xứng hoàn hảo”: nếu bạn đánh dấu một mặt G nào đó và một trong các đỉnh A của nó, thì với bất kỳ mặt nào khác G1 và đỉnh A1 của nó, bạn có thể kết hợp khối đa diện đó với chính nó bằng cách di chuyển trong không gian sao cho mặt G thẳng hàng với G1 và đỉnh A sẽ kết thúc tại điểm A1.

1. 2. Bối cảnh lịch sử.

Năm khối đa diện đều liệt kê ở trên, thường còn được gọi là “các khối Platonic”, đã thu hút trí tưởng tượng của các nhà toán học, nhà huyền học và triết gia thời cổ đại hơn hai nghìn năm trước. Người Hy Lạp cổ đại thậm chí còn thiết lập một sự tương ứng thần bí giữa khối tứ diện, khối lập phương, khối tám mặt và khối hai mươi mặt và bốn nguyên tắc tự nhiên - lửa, đất, không khí và nước. Đối với khối đa diện đều thứ năm, khối mười hai mặt, họ coi nó là hình dạng của Vũ trụ. Những ý tưởng này không chỉ là chuyện của quá khứ. Và bây giờ, hai thiên niên kỷ sau, nhiều người bị thu hút bởi nguyên tắc thẩm mỹ cơ bản.

Bốn khối đa diện đầu tiên đã được biết đến từ lâu trước Plato. Các nhà khảo cổ đã tìm thấy một khối mười hai mặt được tạo ra trong nền văn minh Etruscan ít nhất 500 năm trước Công nguyên. đ. Nhưng, rõ ràng, trong trường phái của Plato, khối mười hai mặt được phát hiện một cách độc lập. Có một truyền thuyết về học trò của Plato là Hippases, người đã chết trên biển vì tiết lộ bí mật về “quả bóng có mười hai hình ngũ giác”.

Kể từ thời Plato và Euclid, người ta đã biết rõ rằng có chính xác năm loại khối đa diện đều.

Hãy chứng minh sự thật này. Giả sử tất cả các mặt của một khối đa diện nhất định là n-giác đều và k là số mặt kề với một đỉnh (tất cả các đỉnh đều như nhau). Hãy xem xét đỉnh A của khối đa diện của chúng ta. Cho M1, M2,. , Mk - các đầu của k cạnh đi ra khỏi nó; do các góc nhị diện ở các cạnh này bằng nhau nên AM1M2Mk là hình chóp đều: khi quay một góc 360°/k quanh độ cao AN, đỉnh M đi vào M, đỉnh M1 vào M2. Mk đến M1.

Hãy so sánh hai tam giác cân AM1M2 và HM1M2 có chung một đáy và cạnh bên AM1 lớn hơn HM1 nên M1AM2.

Tứ diện 3 3 4 4 6

Khối lập phương 4 3 8 6 12

Bát diện 3 4 6 8 12

Khối mười hai mặt 5 3 20 12 30

Hai mặt 3 5 12 20 30

1. 3. Xây dựng khối đa diện đều.

Tất cả các khối đa diện tương ứng có thể được xây dựng bằng cách sử dụng khối lập phương làm cơ sở.

Để có được một tứ diện đều, chỉ cần lấy bốn đỉnh không liền kề của một khối lập phương và cắt các hình chóp ra khỏi nó bằng bốn mặt phẳng, mỗi mặt phẳng đi qua ba trong số các đỉnh đã chọn

Một tứ diện như vậy có thể được nội tiếp trong hình lập phương theo hai cách.

Giao điểm của hai tứ diện đều như vậy chỉ là một bát diện đều: một khối đa diện gồm tám hình tam giác có các đỉnh nằm ở tâm các mặt của khối lập phương.

2. Tính chất của khối đa diện đều.

2. 1. Hình cầu và khối đa diện đều.

Các đỉnh của bất kỳ đa diện đều nào nằm trên mặt cầu (điều này hầu như không có gì đáng ngạc nhiên nếu chúng ta nhớ rằng các đỉnh của bất kỳ đa diện đều nào cũng nằm trên đường tròn). Ngoài quả cầu này, được gọi là "quả cầu được mô tả", còn có hai quả cầu quan trọng hơn. Một trong số chúng, “hình cầu trung tuyến”, đi qua trung điểm của tất cả các cạnh, và cái còn lại, “hình cầu nội tiếp”, chạm vào tất cả các mặt tại tâm của chúng. Cả ba mặt cầu đều có một tâm chung gọi là tâm của khối đa diện.

Bán kính của hình cầu nội tiếp Tên của khối đa diện Bán kính của hình cầu nội tiếp

tứ diện

khối mười hai mặt

icosahedron

2. 1. Khối đa diện tự thẳng hàng.

Hình lập phương, khối tứ diện và bát diện có những cách tự sắp xếp nào (các phép quay tự chuyển thành chính chúng)? Lưu ý rằng một điểm nhất định, tâm của khối đa diện, biến đổi thành chính nó để tự sắp xếp, sao cho tất cả các cách tự sắp xếp đều có một điểm cố định chung.

Chúng ta hãy xem có những loại chuyển động quay nào trong không gian với một điểm cố định A. Hãy chứng minh rằng một chuyển động quay như vậy nhất thiết phải là chuyển động quay một góc nhất định xung quanh một đường thẳng nào đó đi qua điểm A. Nó đủ cho chuyển động F(c F) của chúng ta (A) = A) để biểu thị một đường thẳng cố định. Bạn có thể tìm như sau: Xét ba điểm M1, M2 = F(M1) và M3 = F(M2), khác điểm cố định A, vẽ một mặt phẳng đi qua chúng và thả một AN vuông góc lên đó - đây sẽ là đường thẳng mong muốn. (Nếu M3 = M1 thì đường thẳng của ta đi qua chính giữa đoạn M1M2, và F là đối xứng trục: quay một góc 180°).

Vì vậy, sự tự sắp xếp của một khối đa diện nhất thiết phải là một phép quay quanh một trục đi qua tâm của khối đa diện. Trục này cắt khối đa diện của chúng ta ở một đỉnh hoặc tại điểm bên trong của một cạnh hoặc mặt. Do đó, tính năng tự căn chỉnh của chúng ta chuyển một đỉnh, cạnh hoặc mặt thành chính nó, nghĩa là nó tự chuyển thành một đỉnh, giữa một cạnh hoặc tâm của một mặt. Kết luận: Chuyển động của khối lập phương, tứ diện hoặc bát diện, kết hợp với chính nó, là chuyển động quay quanh một trục thuộc một trong ba loại: tâm của khối đa diện là đỉnh, tâm của khối đa diện là giữa cạnh, tâm của khối đa diện là tâm của mặt.

Nói chung, nếu một khối đa diện thẳng hàng với chính nó khi quay quanh một đường thẳng một góc 360°/m thì đường thẳng này được gọi là trục đối xứng bậc m.

2. 2. Chuyển động và tính đối xứng.

Mối quan tâm chính của các khối đa diện đều là do chúng có số lượng lớn các đối xứng.

Khi xem xét khả năng tự sắp xếp của các khối đa diện, chúng ta có thể bao gồm không chỉ các phép quay mà còn bao gồm bất kỳ chuyển động nào biến khối đa diện thành chính nó. Ở đây chuyển động là bất kỳ sự biến đổi nào của không gian nhằm bảo toàn khoảng cách theo cặp giữa các điểm.

Ngoài chuyển động quay, số chuyển động còn phải bao gồm chuyển động gương. Trong số đó có sự đối xứng so với mặt phẳng (sự phản xạ), cũng như thành phần của sự phản xạ so với mặt phẳng và chuyển động quay quanh một đường thẳng vuông góc với nó (đây là dạng chuyển động gương chung có một điểm cố định). Tất nhiên, những chuyển động như vậy không thể được thực hiện bằng chuyển động liên tục của khối đa diện trong không gian.

Chúng ta hãy xem xét kỹ hơn sự đối xứng của tứ diện. Mọi đường thẳng đi qua một đỉnh và tâm của tứ diện đều đi qua tâm của mặt đối diện. Một góc quay 120 hoặc 240 độ quanh đường thẳng này là một trong những sự đối xứng của tứ diện. Vì tứ diện có 4 đỉnh (và 4 mặt) nên chúng ta có tổng cộng 8 đối xứng trực tiếp. Mọi đường thẳng đi qua tâm và trung điểm của một cạnh của tứ diện đều đi qua trung điểm của cạnh đối diện. Một góc quay 180 độ (nửa vòng) xung quanh một đường thẳng như vậy cũng có tính đối xứng. Vì tứ diện có 3 cặp cạnh nên ta có thêm 3 đối xứng trực tiếp. Do đó, tổng số đối xứng trực tiếp, bao gồm cả phép biến đổi danh tính, đạt tới 12. Có thể chứng minh rằng không có đối xứng trực tiếp nào khác và có 12 đối xứng ngược. Như vậy, tứ diện cho phép có tổng cộng 24 phép đối xứng.

Sự đối xứng trực tiếp của các khối đa diện đều còn lại có thể được tính bằng công thức [(q - 1)N0 + N1 + (p - 1)N2]/2 + 1, trong đó p là số cạnh của đa giác đều là các mặt của đa diện, q là số mặt kề nhau của mỗi đỉnh, N0 là số đỉnh, N1 là số cạnh và N2 là số mặt của mỗi khối đa diện.

Khối lục giác và bát diện đều có 24 đối xứng, khối hai mươi mặt và khối mười hai mặt có 60 đối xứng mỗi khối.

Tất cả các khối đa diện đều có các mặt phẳng đối xứng (tứ diện có 6 mặt phẳng, khối lập phương và bát diện có 9 mặt phẳng, khối 20 mặt và khối mười hai mặt mỗi mặt có 15 mặt phẳng).

2. 3. Khối đa diện sao.

Ngoài các khối đa diện thông thường, các khối đa diện hình sao còn có hình dáng đẹp. Chỉ có bốn người trong số họ. Hai cái đầu tiên được phát hiện bởi J. Kepler (1571 - 1630), và hai cái còn lại được xây dựng gần 200 năm sau bởi L. Poinsot (1777 - 1859). Đó là lý do tại sao các khối đa diện hình sao đều được gọi là vật thể Kepler-Poinsot. Chúng thu được từ các khối đa diện thông thường bằng cách mở rộng các mặt hoặc các cạnh của chúng. Nhà hình học người Pháp Poinsot vào năm 1810 đã xây dựng bốn khối đa diện hình sao đều: khối mười hai mặt hình sao nhỏ, khối mười hai mặt hình sao lớn, khối mười hai mặt lớn và khối mười hai mặt lớn. Bốn khối đa diện này có các mặt giao nhau với các khối đa diện đều và hai trong số chúng có mỗi mặt là một đa giác tự cắt nhau. Nhưng Poinsot không thể chứng minh rằng không có khối đa diện đều nào khác.

Một năm sau (1811), nhà toán học người Pháp Augustin Louis Cauchy (1789 - 1857) đã làm được điều này. Ông đã lợi dụng thực tế là, theo định nghĩa của một khối đa diện đều, nó có thể được xếp chồng lên chính nó sao cho một mặt tùy ý của nó trùng với một mặt đã chọn trước đó. Từ đó suy ra rằng tất cả các mặt của khối đa diện hình sao đều cách đều một số điểm-tâm của hình cầu nội tiếp trong khối đa diện.

Các mặt phẳng của các mặt của một khối đa diện hình sao, giao nhau, cũng tạo thành một khối đa diện lồi đều, tức là một khối Platonic được mô tả xung quanh cùng một hình cầu. Cauchy gọi khối Platonic này là lõi của khối đa diện hình sao này. Do đó, có thể thu được một khối đa diện hình sao bằng cách tiếp tục các mặt phẳng của một trong các khối Platonic.

Không thể thu được các khối đa diện hình sao từ một khối tứ diện, khối lập phương hoặc khối bát diện. Hãy xem xét khối mười hai mặt. Việc tiếp tục các cạnh của nó dẫn đến việc thay thế mỗi mặt bằng một hình ngũ giác đều có hình sao, và kết quả là một khối mười hai mặt hình sao nhỏ.

Khi tiếp tục các mặt của khối mười hai mặt, có thể xảy ra hai trường hợp sau: 1) nếu xét các hình ngũ giác đều, thì chúng ta thu được một khối mười hai mặt lớn.

2) nếu chúng ta coi các hình ngũ giác hình sao là các mặt thì chúng ta sẽ có một khối mười hai mặt hình sao lớn.

Khối hai mươi mặt có hình dạng ngôi sao duy nhất. Khi cạnh của một khối hai mươi mặt đều được kéo dài ra, ta sẽ thu được một khối hai mươi mặt lớn.

Như vậy, có bốn loại khối đa diện hình sao đều.

Các khối đa diện hình sao có tính trang trí rất cao, cho phép chúng được sử dụng rộng rãi trong ngành trang sức để sản xuất các loại trang sức.

Nhiều dạng khối đa diện hình sao được tự nhiên gợi ý. Bông tuyết là khối đa diện hình ngôi sao. Từ xa xưa, con người đã cố gắng mô tả tất cả các loại bông tuyết có thể có và biên soạn các tập bản đồ đặc biệt. Hàng ngàn loại bông tuyết khác nhau hiện đã được biết đến.

Phần kết luận

Công trình bao gồm các chủ đề sau: khối đa diện đều, xây dựng khối đa diện đều, tự sắp thẳng hàng, chuyển động và đối xứng, khối đa diện hình sao và tính chất của chúng. Chúng ta đã biết rằng chỉ có năm khối đa diện đều và bốn khối đa diện đều hình sao, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau.

Việc nghiên cứu chất rắn Platonic và các số liệu liên quan vẫn tiếp tục cho đến ngày nay. Mặc dù vẻ đẹp và tính đối xứng là động lực chính cho nghiên cứu hiện đại nhưng chúng cũng có một số ý nghĩa khoa học, đặc biệt là trong tinh thể học. Các tinh thể muối ăn, natri thioantimonide và phèn crom xuất hiện trong tự nhiên ở dạng lập phương, tứ diện và bát diện tương ứng. Khối hai mươi mặt và khối mười hai mặt không được tìm thấy trong các dạng tinh thể, nhưng chúng có thể được quan sát thấy trong các dạng sinh vật biển cực nhỏ được gọi là radiolarian.

Ý tưởng của Plato và Kepler về mối liên hệ của các khối đa diện đều với cấu trúc hài hòa của thế giới trong thời đại chúng ta đã được tiếp tục trong một giả thuyết khoa học thú vị vào đầu những năm 80. được bày tỏ bởi các kỹ sư Moscow V. Makarov và V. Morozov. Họ tin rằng lõi Trái đất có hình dạng và đặc tính của một tinh thể đang phát triển, điều này ảnh hưởng đến sự phát triển của mọi quá trình tự nhiên diễn ra trên hành tinh. Các tia của tinh thể này, hay đúng hơn là trường lực của nó, xác định cấu trúc khối 20 mặt-mười hai mặt của Trái đất. Nó thể hiện ở chỗ trong vỏ trái đất xuất hiện hình chiếu của các khối đa diện đều nội tiếp trên quả địa cầu: khối hai mươi mặt và khối mười hai mặt.

Nhiều mỏ khoáng sản trải dài dọc theo mạng lưới khối 20 mặt-mười hai mặt; 62 đỉnh và trung điểm của các cạnh của khối đa diện, được các tác giả gọi là nút, có một số tính chất cụ thể giúp giải thích một số hiện tượng khó hiểu. Đây là những trung tâm của nền văn hóa và văn minh cổ đại: Peru, Bắc Mông Cổ, Haiti, văn hóa Ob và những nơi khác. Tại những điểm này, người ta quan sát được áp suất khí quyển tối đa và tối thiểu cũng như các dòng xoáy khổng lồ của Đại dương Thế giới. Các nút này chứa hồ Loch Ness và Tam giác quỷ Bermuda. Các nghiên cứu sâu hơn về Trái đất có thể xác định thái độ đối với giả thuyết khoa học này, trong đó, có thể thấy, các khối đa diện đều chiếm một vị trí quan trọng.

Cấu trúc của khối đa diện đều rất thuận tiện cho việc nghiên cứu nhiều phép biến đổi của khối đa diện thành chính nó (xoay, đối xứng, v.v.). Các nhóm biến đổi thu được (chúng được gọi là nhóm đối xứng) hóa ra rất thú vị theo quan điểm của lý thuyết nhóm hữu hạn. Sự đối xứng tương tự giúp tạo ra một loạt câu đố dưới dạng khối đa diện thông thường, bắt đầu bằng “khối Rubik” và “kim tự tháp Moldavian”.

Các nhà điêu khắc, kiến trúc sư và nghệ sĩ cũng tỏ ra rất quan tâm đến các dạng khối đa diện đều. Tất cả họ đều ngạc nhiên trước sự hoàn hảo và hài hòa của các khối đa diện. Leonardo da Vinci (1452 - 1519) quan tâm đến lý thuyết khối đa diện và thường miêu tả chúng trên các bức vẽ của mình. Trong bức tranh “Bữa tối cuối cùng”, Salvador Dali đã miêu tả Chúa Giêsu Kitô cùng các môn đệ của mình trên phông nền của một khối mười hai mặt trong suốt khổng lồ.

Nội dung của bài viết

đa diện, một phần không gian được giới hạn bởi một tập hợp gồm một số hữu hạn các đa giác phẳng được kết nối sao cho mỗi cạnh của bất kỳ đa giác nào đều là cạnh của chính xác một đa giác khác (được gọi là liền kề), với chính xác một chu kỳ đa giác tồn tại xung quanh mỗi đỉnh. Các đa giác này được gọi là các mặt, các cạnh của chúng được gọi là các cạnh và các đỉnh của chúng được gọi là các đỉnh của khối đa diện.

Trong bộ lễ phục. Hình 1 cho thấy một số khối đa diện nổi tiếng. Hai cái đầu tiên đóng vai trò là ví dụ R-kim tự tháp than, tức là khối đa diện gồm có R- một tam giác gọi là đáy, và R các tam giác kề nhau có một đỉnh chung (gọi là đỉnh của hình chóp). Tại R = 3 (cmt. cơm. 1, MỘT) bất kỳ mặt nào của kim tự tháp đều có thể dùng làm đáy. Một kim tự tháp có đáy có hình dạng bình thường R-gon được gọi là thường xuyên R-kim tự tháp than. Vì vậy, chúng ta có thể nói về hình vuông, hình ngũ giác đều, v.v. kim tự tháp. Trong bộ lễ phục. 1, V., 1,G và 1, dđưa ra các ví dụ về một loại khối đa diện nhất định, các đỉnh của chúng có thể được chia thành hai tập hợp có cùng số điểm; điểm của mỗi bộ này là các đỉnh R-gon, và các mặt phẳng của cả hai P-các góc song song. Nếu hai điều này R-gon (cơ sở) bằng nhau và nằm sao cho các đỉnh của một R R-giác bằng các đoạn thẳng song song thì khối đa diện đó gọi là R- lăng kính cacbon. Ví dụ về hai R- lăng kính góc có thể đóng vai trò là lăng kính tam giác ( R= 3) trong hình. 1, V. và một lăng kính ngũ giác ( R= 5) trong hình. 1, G. Nếu các căn cứ được đặt sao cho đỉnh của một R-gon được nối với các đỉnh của một cái khác R-giác của một đường đứt nét ngoằn ngoèo gồm 2 Rđoạn thẳng như hình vẽ. 1, d, thì khối đa diện như vậy được gọi là R- phản lăng kính carbon.

Ngoài hai lý do, R- lăng kính carbon có sẵn R mặt - hình bình hành. Nếu các hình bình hành có dạng hình chữ nhật thì lăng kính được gọi là đường thẳng và nếu các đáy đều đều R-gons thì lăng kính được gọi là quyền chính quy R- lăng kính cacbon. R- phản lăng kính cacbon có (2 P+ 2) khuôn mặt: 2 R mặt tam giác và hai P- cơ sở than. Nếu các cơ sở là những cơ sở đều đặn R- các giác, và đường thẳng nối tâm của chúng vuông góc với các mặt phẳng của chúng thì phản lăng kính gọi là đường thẳng đều R- phản lăng kính carbon.

Trong định nghĩa về khối đa diện, mệnh đề cuối cùng được đưa ra nhằm loại trừ khỏi việc xem xét những dị thường như hai hình chóp có cùng một đỉnh. Bây giờ chúng tôi đưa ra một ràng buộc bổ sung đối với tập hợp các polytop được chấp nhận bằng cách yêu cầu không có hai mặt nào giao nhau, như trong Hình 2. 1, e. Bất kỳ khối đa diện nào thỏa mãn yêu cầu này đều chia không gian thành hai phần, một phần là hữu hạn và được gọi là “nội bộ”. Phần còn lại được gọi là bên ngoài.

Một khối đa diện được gọi là lồi nếu không có một đoạn thẳng nào nối hai điểm bất kỳ của nó chứa các điểm thuộc không gian bên ngoài. Khối đa diện trong hình. 1, MỘT, 1,b, 1,V. và 1, d lồi và lăng kính ngũ giác ở hình 2. 1, G không lồi, vì, ví dụ, đoạn PQ chứa các điểm nằm trong không gian bên ngoài của lăng kính.

TUYỆT VỜI THƯỜNG XUYÊN

Một khối đa diện lồi được gọi là đều nếu nó thỏa mãn hai điều kiện sau:

283(i) tất cả các mặt của nó đều là các đa giác đều bằng nhau;

(ii) mỗi đỉnh có cùng số mặt liền kề với nó.

Nếu tất cả các cạnh đều đúng R-gon và q trong đó liền kề với mỗi đỉnh thì khối đa diện đều đó được ký hiệu là ( P, q). Ký hiệu này được đề xuất bởi L. Schläfli (1814–1895), một nhà toán học Thụy Sĩ, người chịu trách nhiệm về nhiều kết quả hay trong hình học và giải tích toán học.

Có những khối đa diện không lồi có các mặt giao nhau và được gọi là "khối đa diện hình sao đều". Vì chúng ta đã đồng ý không xem xét các khối đa diện như vậy, nên khi nói đến các khối đa diện đều, chúng ta sẽ chỉ muốn nói đến các khối đa diện đều lồi.

Chất rắn Platon.

Trong bộ lễ phục. 2 cho thấy khối đa diện đều. Đơn giản nhất trong số đó là một tứ diện đều, các mặt của chúng là bốn hình tam giác đều và ba mặt liền kề với mỗi đỉnh. Tứ diện tương ứng với ký hiệu (3, 3). Đây không gì khác hơn là một trường hợp đặc biệt của hình chóp tam giác. Khối đa diện đều nổi tiếng nhất là khối lập phương (đôi khi được gọi là hình lục giác đều) - một lăng kính vuông thẳng, tất cả sáu mặt đều là hình vuông. Vì mỗi đỉnh có 3 ô vuông liền kề nên khối lập phương được ký hiệu là (4, 3). Nếu hai hình chóp vuông bằng nhau có các mặt có hình tam giác đều được kết hợp ở đáy của chúng thì kết quả là một khối đa diện gọi là bát diện đều. Nó được giới hạn bởi tám hình tam giác đều, mỗi đỉnh tiếp giáp với bốn hình tam giác, và do đó ký hiệu (3, 4) tương ứng với nó. Một bát diện đều cũng có thể được coi là một trường hợp đặc biệt của phản lăng trụ tam giác đều trực tiếp. Bây giờ chúng ta hãy xem xét một hình lăng trụ đứng ngũ giác đều, các mặt của nó có hình tam giác đều và hai hình chóp ngũ giác đều, đáy của chúng bằng đáy của phản lăng trụ và các mặt có hình tam giác đều. Nếu những kim tự tháp này được gắn vào một phản lăng kính, căn chỉnh các đáy của chúng, thì chúng ta sẽ có một khối đa diện đều khác. Hai mươi mặt của nó có dạng hình tam giác đều, mỗi đỉnh có năm mặt kề nhau. Khối đa diện như vậy được gọi là khối đa diện đều và được ký hiệu là (3, 5). Ngoài bốn khối đa diện đều nêu trên, còn có một khối nữa - một khối mười hai mặt đều, được giới hạn bởi mười hai mặt ngũ giác; mỗi đỉnh của nó liền kề với ba mặt nên khối mười hai mặt được ký hiệu là (5, 3).

Người Hy Lạp cổ đại cũng nghiên cứu nhiều tính chất hình học của khối Platonic; thành quả nghiên cứu của họ có thể được tìm thấy trong cuốn sách thứ 13 Đã bắt đầu Euclid. Việc nghiên cứu chất rắn Platonic và các số liệu liên quan vẫn tiếp tục cho đến ngày nay. Mặc dù vẻ đẹp và tính đối xứng là động lực chính cho nghiên cứu hiện đại nhưng chúng cũng có một số ý nghĩa khoa học, đặc biệt là trong tinh thể học. Các tinh thể muối ăn, natri thioantimonide và phèn crom xuất hiện trong tự nhiên ở dạng lập phương, tứ diện và bát diện tương ứng. Khối hai mươi mặt và khối mười hai mặt không được tìm thấy trong các dạng tinh thể, nhưng chúng có thể được quan sát thấy trong các dạng sinh vật biển cực nhỏ được gọi là radiolarian.

Số khối đa diện đều.

Thật tự nhiên khi đặt câu hỏi liệu ngoài các khối Platonic còn có các khối đa diện đều khác hay không. Như những cân nhắc đơn giản sau đây cho thấy, câu trả lời phải là phủ định. Cho phép ( P, q) là một khối đa diện đều tùy ý. Vì các cạnh của nó là chính xác R-giác, các góc trong của chúng, như dễ thấy, đều bằng nhau (180 – 360/ R) hoặc 180 (1 – 2/ R) độ. Vì khối đa diện ( P, q) lồi thì tổng các góc trong dọc theo các mặt kề với bất kỳ đỉnh nào của nó phải nhỏ hơn 360 độ. Nhưng mỗi đỉnh đều liền kề q các mặt, do đó bất đẳng thức phải được thỏa mãn

Không khó để nhận ra điều đó P Và q phải lớn hơn 2. Thay vào (1) R= 3, chúng tôi thấy rằng các giá trị hợp lệ duy nhất là q trong trường hợp này là 3, 4 và 5, tức là chúng ta thu được khối đa diện (3, 3), (3, 4) và (3, 5). Tại R= 4 là giá trị hợp lệ duy nhất q là 3, tức là khối đa diện (4, 3), với R= 5 bất đẳng thức (1) cũng chỉ thỏa mãn q= 3, tức là đa diện (5, 3). Tại P> 5 giá trị hợp lệ q không tồn tại. Do đó, không có khối đa diện đều nào khác ngoại trừ khối Platonic.

Tất cả năm khối đa diện đều được liệt kê trong bảng dưới đây. Ba cột cuối cùng cho biết N 0 – số đỉnh, N 1 – số cạnh và N 2 – số mặt của mỗi khối đa diện.

Thật không may, định nghĩa về khối đa diện đều được đưa ra trong nhiều sách giáo khoa hình học là chưa đầy đủ. Một lỗi phổ biến là định nghĩa chỉ yêu cầu thỏa mãn điều kiện (i) ở trên mà bỏ qua điều kiện (ii). Trong khi đó, điều kiện (ii) là hoàn toàn cần thiết, dễ dàng kiểm chứng nhất bằng cách xét khối đa diện lồi thỏa mãn điều kiện (i) nhưng không thỏa mãn điều kiện (ii). Ví dụ đơn giản nhất của loại này có thể được xây dựng bằng cách xác định mặt của một tứ diện đều với mặt của một tứ diện khác, đồng dạng với mặt thứ nhất. Kết quả là chúng ta có được một khối đa diện lồi, sáu mặt của chúng là các hình tam giác đều bằng nhau. Tuy nhiên, một số đỉnh có ba mặt liền kề với chúng, trong khi những đỉnh khác có bốn mặt, vi phạm điều kiện (ii).

NĂM POLYHEDES THƯỜNG XUYÊN
Tên	Bản ghi âm của Schläfli	N 0 (số đỉnh)	N 1 (số xương sườn)	N 2 (số lượng khuôn mặt)
tứ diện
khối lập phương
bát diện
icosahedron
khối mười hai mặt

Tính chất của khối đa diện đều.

Khối đa diện kép.

Xét một khối đa diện đều ( P, q) và hình cầu ở giữa của nó S. Điểm giữa của mỗi cạnh chạm vào hình cầu. Thay thế mỗi cạnh bằng một đoạn thẳng vuông góc với đường thẳng tiếp tuyến với S tại cùng một điểm chúng tôi nhận được N 1 cạnh của khối đa diện kép thành khối đa diện ( P, q). Không khó để chứng minh rằng các mặt của khối đa diện kép đều đều q-gons và mỗi đỉnh liền kề nhau R những khuôn mặt. Do đó, khối đa diện ( P, q) là đối ngẫu của một khối đa diện đều ( q, P). Khối đa diện (3, 3) đối ngẫu với khối đa diện khác (3, 3), đồng dạng với khối đa diện ban đầu (do đó (3, 3) gọi là đa diện tự đôi), khối đa diện (4, 3) lưỡng diện với khối đa diện đó. khối đa diện (3, 4) và khối đa diện (5, 3) là khối đa diện kép – khối đa diện (3, 5). Trong bộ lễ phục. 3 khối đa diện (4, 3) và (3, 4) được thể hiện đối ngẫu với nhau. Ngoài ra, mỗi đỉnh, mỗi cạnh và mỗi mặt của khối đa diện ( P, q) tương ứng với mặt duy nhất, cạnh duy nhất và đỉnh duy nhất của khối đa diện kép ( q, P). Do đó, nếu ( P, q) Nó có N 0 đỉnh, N 1 xương sườn và N 2 mặt thì ( q, P) Nó có N 2 đỉnh, N 1 xương sườn và N 0 khuôn mặt.

Vì mỗi N 2 mặt của khối đa diện đều ( P, q) giới hạn R các cạnh và mỗi cạnh chung cho đúng hai mặt thì tổng cộng có pN 2/2 xương sườn vậy N 1 = pN 2/2. Khối đa diện kép ( q, P) cũng có xương sườn N 1 và N 0 khuôn mặt, vậy N 1 = qN 0 /2. Vậy những con số N 0 , N 1 và N 2 cho mọi khối đa diện đều ( P, q) có liên hệ bởi quan hệ

Đối diện.

Mối quan tâm chính của các khối đa diện đều là do chúng có số lượng lớn các đối xứng. Khi nói đến tính đối xứng (hoặc phép biến đổi đối xứng) của một khối đa diện, chúng ta muốn nói đến chuyển động của nó như một vật rắn trong không gian (ví dụ, quay quanh một đường thẳng nhất định, phản xạ so với một mặt phẳng nhất định, v.v.), rời khỏi tập hợp các đỉnh, các cạnh và các mặt của khối đa diện không thay đổi. Nói cách khác, dưới tác dụng của một phép biến đổi đối xứng, một đỉnh, cạnh hoặc mặt vẫn giữ nguyên vị trí ban đầu hoặc được chuyển đến vị trí ban đầu của một đỉnh, cạnh khác hoặc mặt khác.

Có một tính đối xứng chung cho tất cả các khối đa diện. Chúng ta đang nói về một sự chuyển đổi bản sắc để lại bất kỳ điểm nào ở vị trí ban đầu của nó. Chúng ta gặp một ví dụ ít tầm thường hơn về tính đối xứng trong trường hợp đường thẳng R- lăng kính cacbon. Cho phép tôi- đường thẳng nối tâm của các đáy. Quay lại tôi với bội số nguyên bất kỳ của góc 360/ Rđộ là sự đối xứng. Hãy để, hơn nữa, P- một mặt phẳng đi qua điểm giữa hai đáy song song với chúng. Sự phản chiếu so với mặt phẳng P(một chuyển động chiếm bất kỳ điểm nào P chính xác Pў , như vậy P cắt đoạn PPў vuông góc và chia nó làm đôi) - một sự đối xứng khác. Kết hợp sự phản xạ so với một mặt phẳng P với việc quay quanh một đường thẳng tôi, chúng ta có được một sự đối xứng khác.

Bất kỳ sự đối xứng nào của khối đa diện đều có thể được biểu diễn dưới dạng sản phẩm của sự phản xạ. Bằng cách thực hiện một số chuyển động của khối đa diện như một vật thể cứng, ở đây chúng tôi muốn nói đến việc thực hiện các chuyển động riêng lẻ theo một thứ tự nhất định được xác định trước. Ví dụ phép quay nêu trên qua một góc 360/ Rđộ quanh một đường thẳng tôi là tích của sự phản xạ so với hai mặt phẳng bất kỳ chứa tôi và tạo thành một góc 180/ so với nhau Rđộ. Một sự đối xứng là tích của một số lượng phản xạ chẵn được gọi là trực tiếp, nếu không nó được gọi là nghịch đảo. Do đó, mọi phép quay quanh một đường thẳng đều có tính đối xứng trực tiếp. Mọi sự phản xạ đều có tính đối xứng ngược.

Chúng ta hãy xem xét chi tiết hơn các tính đối xứng của tứ diện, tức là đa diện đều (3, 3). Mọi đường thẳng đi qua một đỉnh và tâm của tứ diện đều đi qua tâm của mặt đối diện. Một góc quay 120 hoặc 240 độ quanh đường thẳng này là một trong những sự đối xứng của tứ diện. Vì tứ diện có 4 đỉnh (và 4 mặt) nên chúng ta có tổng cộng 8 đối xứng trực tiếp. Mọi đường thẳng đi qua tâm và trung điểm của một cạnh của tứ diện đều đi qua trung điểm của cạnh đối diện. Một góc quay 180 độ (nửa vòng) xung quanh một đường thẳng như vậy cũng có tính đối xứng. Vì tứ diện có 3 cặp cạnh nên ta có thêm 3 đối xứng trực tiếp. Do đó, tổng số đối xứng trực tiếp, bao gồm cả phép biến đổi danh tính, đạt tới 12. Có thể chứng minh rằng không có đối xứng trực tiếp nào khác và có 12 đối xứng ngược. Như vậy, tứ diện cho phép có tổng cộng 24 phép đối xứng. Để rõ ràng, sẽ rất hữu ích khi xây dựng một mô hình bìa cứng của một tứ diện đều và đảm bảo rằng tứ diện đó thực sự có 24 đối xứng. Các phát triển có thể được cắt từ bìa cứng mỏng và gấp lại, dán lại với nhau thành năm khối đa diện đều, được thể hiện trong Hình 2. 4.

Sự đối xứng trực tiếp của các khối đa diện đều còn lại có thể được mô tả không phải riêng lẻ mà tất cả cùng nhau. Hãy để chúng tôi đồng ý hiểu bởi ( P, q) mọi khối đa diện đều ngoại trừ (3, 3). Đường thẳng đi qua tâm ( P, q) và bất kỳ đỉnh nào đi qua đỉnh đối diện và bất kỳ phép quay nào với bội số nguyên của 360/ qđộ xung quanh đường này là sự đối xứng. Do đó, đối với mỗi dòng như vậy đều tồn tại, bao gồm cả phép biến đổi danh tính, ( q– 1) sự đối xứng khác nhau. Mỗi đường thẳng như vậy nối hai N 0 đỉnh; do đó tổng số đường thẳng đó là N 0/2, mang lại ( q – 1) > Nđối xứng 0/2. Ngoài ra, đường thẳng đi qua tâm của khối đa diện ( P, q) và tâm của bất kỳ mặt nào cũng đi qua tâm của mặt đối diện và mọi phép quay quanh đường thẳng đó với bội số nguyên của 360/ Rđộ là sự đối xứng. Vì tổng số dòng như vậy bằng N 2/2, ở đâu N 2 – số mặt của khối đa diện ( P, q), chúng tôi nhận được ( P – 1) N 2/2 sự đối xứng khác nhau, bao gồm cả phép biến đổi nhận dạng. Cuối cùng, một đường thẳng đi qua tâm và điểm giữa của bất kỳ cạnh nào của khối đa diện ( P, q), đi qua điểm giữa của cạnh đối diện và đối xứng là nửa vòng quanh đường thẳng này. Vì có N 1/2 dòng như vậy, ở đâu N 1 – số cạnh của khối đa diện ( P, q), chúng tôi nhận được nhiều hơn Nđối xứng 1/2. Có tính đến sự chuyển đổi danh tính, chúng tôi có được

đối xứng trực tiếp. Không có sự đối xứng trực tiếp nào khác và cũng có rất nhiều sự đối xứng ngược.

Mặc dù công thức (3) không thu được cho khối đa diện (3, 3), nhưng vẫn dễ dàng chứng minh rằng nó cũng đúng với đa diện đó. Như vậy, khối đa diện (3, 3) có 12 đối xứng trực tiếp, khối đa diện (4, 3) và (3, 4) có 24 đối xứng, khối đa diện (5, 3) và (3, 5) có 60 đối xứng.

Những độc giả quen thuộc với đại số trừu tượng sẽ hiểu rằng tính đối xứng của khối đa diện ( P, q) tạo thành một nhóm theo “phép nhân” được xác định ở trên. Trong nhóm này, các đối xứng trực tiếp tạo thành một nhóm con của chỉ số 2 và các đối xứng ngược không tạo thành một nhóm, vì chúng vi phạm tính chất đóng và không chứa phép biến đổi đồng nhất (phần tử đơn vị của nhóm). Thông thường, nhóm đối xứng trực tiếp được gọi là nhóm khối đa diện và nhóm đối xứng hoàn chỉnh được gọi là nhóm mở rộng của nó. Từ các tính chất của khối đa diện kép đã thảo luận ở trên, rõ ràng là mọi khối đa diện đều và khối đa diện kép của nó đều có cùng một nhóm. Nhóm tứ diện được gọi là nhóm tứ diện, nhóm lập phương và bát diện được gọi là nhóm bát diện, và nhóm mười hai mặt và hai mươi mặt được gọi là nhóm hai mươi mặt. Chúng đẳng cấu với nhóm xen kẽ MỘT 4 trong bốn biểu tượng, nhóm đối xứng S 4 trong bốn biểu tượng và nhóm xen kẽ MỘT 5 trong số năm ký tự tương ứng.

CÔNG THỨC CỦA EULER

Nhìn vào bảng, bạn có thể nhận thấy mối quan hệ thú vị giữa số đỉnh N 0, số cạnh N 1 và số mặt N 2 đa diện đều lồi bất kỳ ( P, q). Đó là về tỷ lệ

Thay các biểu thức thu được vào các công thức (3) và (4), chúng ta thu được số lượng đối xứng trực tiếp của khối đa diện ( P, q) bằng

Số này cũng có thể được viết dưới một trong các dạng tương đương: qN 0 , 2N 1 hoặc pN 2 .

Phạm vi áp dụng công thức Euler.

Tầm quan trọng của công thức Euler được nâng cao bởi thực tế là nó không chỉ có thể áp dụng cho chất rắn Platonic mà còn cho bất kỳ khối đa diện đồng cấu nào của hình cầu ( cmt. CỘNG ĐỒNG). Tuyên bố này được chứng minh như sau.

Cho phép P– bất kỳ khối đa diện nào đồng cấu với một hình cầu, với N 0 đỉnh, N 1 xương sườn và N 2 mặt; cho phép c = N 0 – N 1 + N 2 – Đặc tính Euler của khối đa diện P. Cần phải chứng minh rằng c= 2. Vì R là đồng cấu với một mặt cầu, chúng ta có thể loại bỏ một mặt và biến đổi phần còn lại thành một số cấu hình trên mặt phẳng (ví dụ, trong Hình 5, MỘT và 5, b bạn nhìn thấy một lăng kính với mặt phẳng phía trước của nó bị loại bỏ). "Cấu hình phẳng" là một mạng gồm các điểm và đoạn thẳng tương ứng được gọi là "đỉnh" và "cạnh", với các đỉnh đóng vai trò là điểm cuối của các cạnh. Chúng ta coi các đỉnh và cạnh của hình dạng mà chúng ta đang xem xét là các đỉnh và cạnh bị dịch chuyển và biến dạng của khối đa diện. Vì vậy cấu hình này có N 0 đỉnh và N 1 xương sườn Nghỉ ngơi N 2 – 1 mặt của khối đa diện bị biến dạng thành N 2 – 1 vùng không chồng lấp trên một mặt phẳng được xác định theo cấu hình. Hãy gọi những khu vực này là “khuôn mặt” của cấu hình. Các đỉnh, cạnh và mặt của cấu hình xác định đặc tính Euler, trong trường hợp này bằng c – 1.

Bây giờ chúng ta sẽ tiến hành làm phẳng để nếu mặt bị loại bỏ R-hình vuông thì thế thôi N 2 – 1 mặt cấu hình sẽ lấp đầy nội thất R-gon. Cho phép MỘT– một số đỉnh bên trong R-gon. Hãy giả sử rằng trong MỘT hội tụ r xương sườn Nếu bạn xóa MỘT và đó là tất cả r các cạnh hội tụ trong đó thì số đỉnh sẽ giảm đi 1, các cạnh - bằng r, khuôn mặt – trên r – 1 (cmt. cơm. 5, b và 5, V.). Cấu hình mới Nў 0 = N 0 – 1 đỉnh, Nў 1 = N 1 – r xương sườn và Nў 2 = N 2 – 1 – (r- 1) khuôn mặt; kể từ đây,

Do đó, việc loại bỏ một đỉnh bên trong và các cạnh hội tụ tại nó không làm thay đổi đặc tính Euler của cấu hình. Do đó, bằng cách loại bỏ tất cả các đỉnh và cạnh bên trong hội tụ tại chúng, chúng ta sẽ giảm cấu hình thành R-góc và phần bên trong của nó (Hình 5, G). Nhưng đặc tính Euler sẽ vẫn bằng c– 1, và vì cấu hình có Rđỉnh cao, R các cạnh và 1 mặt, ta được

Như vậy, c= 2 là điều cần chứng minh.

Tiếp theo, chúng ta có thể chứng minh rằng nếu đặc tính Euler của một khối đa diện bằng 2 thì khối đa diện đó là đồng cấu với một hình cầu. Nói cách khác, chúng ta có thể khái quát hóa kết quả thu được ở trên bằng cách chỉ ra rằng một khối đa diện là đồng cấu với một hình cầu khi và chỉ khi đặc tính Euler của nó bằng 2.

Công thức Euler tổng quát.

Để phân loại các khối đa diện khác, người ta sử dụng công thức Euler tổng quát. Nếu một khối đa diện nhất định có 16 đỉnh, 32 cạnh và 16 mặt thì đặc số Euler của nó là 16 – 32 + 16 = 0. Điều này cho phép chúng ta khẳng định rằng khối đa diện này thuộc lớp đa diện đồng cấu với hình xuyến. Một đặc điểm khác biệt của lớp này là đặc tính Euler, bằng 0. Tổng quát hơn, hãy R– khối đa diện với N 0 đỉnh, N 1 xương sườn và N 2 mặt. Họ nói rằng một khối đa diện nhất định là đồng hình với một bề mặt của chi N nếu và chỉ nếu

Cuối cùng, cần lưu ý rằng tình huống trở nên phức tạp hơn đáng kể nếu chúng ta nới lỏng ràng buộc trước đó là không có hai mặt nào của khối đa diện phải giao nhau. Ví dụ, có khả năng tồn tại hai khối đa diện không đồng hình có cùng đặc tính Euler. Chúng nên được phân biệt bằng các đặc tính tôpô khác.

Giới thiệu

Một bề mặt bao gồm các đa giác và bao quanh một số khối hình học được gọi là bề mặt đa diện hoặc khối đa diện.

Khối đa diện là một khối có bề mặt bao gồm một số hữu hạn các đa giác. Các đa giác bao quanh một khối đa diện được gọi là các mặt và các đường giao nhau của các mặt được gọi là các cạnh.

Khối đa diện có thể có cấu trúc đa dạng và rất phức tạp. Các cấu trúc khác nhau, chẳng hạn như những ngôi nhà được xây dựng bằng gạch và khối bê tông, là ví dụ về khối đa diện. Các ví dụ khác có thể được tìm thấy trong số đồ nội thất, chẳng hạn như một cái bàn. Trong hóa học, hình dạng của các phân tử hydrocarbon là một khối tứ diện, hai mươi mặt đều, một khối lập phương. Trong vật lý, tinh thể đóng vai trò là ví dụ về khối đa diện.

Từ xa xưa, quan niệm về cái đẹp đã gắn liền với tính đối xứng. Điều này có lẽ giải thích sự quan tâm của mọi người đối với khối đa diện - những biểu tượng đối xứng đáng kinh ngạc đã thu hút sự chú ý của các nhà tư tưởng xuất sắc, những người ngạc nhiên trước vẻ đẹp, sự hoàn hảo và sự hài hòa của những hình này.

Những đề cập đầu tiên về khối đa diện được biết đến vào ba nghìn năm trước Công nguyên ở Ai Cập và Babylon. Chỉ cần nhớ lại các kim tự tháp Ai Cập nổi tiếng và nổi tiếng nhất trong số đó là Kim tự tháp Cheops. Đây là một kim tự tháp thông thường, ở đáy là một hình vuông có cạnh 233 m và chiều cao lên tới 146,5 m. Không phải ngẫu nhiên mà người ta nói rằng Kim tự tháp Cheops là một chuyên luận thầm lặng về hình học.

Lịch sử của các khối đa diện đều có từ thời cổ đại. Bắt đầu từ thế kỷ thứ 7 trước Công nguyên, các trường phái triết học đã được thành lập ở Hy Lạp cổ đại, trong đó có sự chuyển đổi dần dần từ hình học thực tiễn sang hình học triết học. Lý luận với sự trợ giúp của nó có thể thu được các đặc tính hình học mới có tầm quan trọng lớn trong các trường phái này.

Một trong những trường học đầu tiên và nổi tiếng nhất là trường Pythagore, được đặt theo tên của người sáng lập Pythagoras. Dấu hiệu đặc biệt của Pythagore là ngôi sao năm cánh, trong ngôn ngữ toán học, nó là một hình ngũ giác đều không lồi hoặc hình ngôi sao. Ngôi sao năm cánh được giao khả năng bảo vệ một người khỏi linh hồn ma quỷ.

Người Pythagore tin rằng vật chất bao gồm bốn yếu tố cơ bản: lửa, đất, không khí và nước. Họ cho rằng sự tồn tại của năm khối đa diện đều là do cấu trúc của vật chất và Vũ trụ. Theo quan điểm này, nguyên tử của các nguyên tố chính phải có dạng các vật thể khác nhau:

§ Vũ trụ là một khối mười hai mặt

§ Trái đất - khối lập phương

§ Lửa - tứ diện

§ Nước - khối đa diện

§ Không khí - bát diện

Sau đó, lời dạy của những người theo trường phái Pythagoras về các khối đa diện đều đã được một nhà khoa học Hy Lạp cổ đại khác, nhà triết học duy tâm Plato, phác thảo trong các tác phẩm của ông. Kể từ đó, các khối đa diện đều được gọi là khối Platonic.

Hình khối Platonic là các khối đa diện lồi đồng nhất đều, nghĩa là các khối đa diện lồi, tất cả các mặt và các góc đều bằng nhau và các mặt là đa giác đều. Cùng một số cạnh hội tụ về mỗi đỉnh của một khối đa diện đều. Tất cả các góc nhị diện ở các cạnh và tất cả các góc đa diện ở các đỉnh của một đa giác đều bằng nhau. Hình khối Platonic là một dạng tương tự ba chiều của đa giác đều phẳng.

Lý thuyết khối đa diện là một nhánh hiện đại của toán học. Nó liên quan chặt chẽ đến cấu trúc liên kết, lý thuyết đồ thị và có tầm quan trọng lớn cho cả nghiên cứu lý thuyết về hình học và ứng dụng thực tế trong các ngành toán học khác như đại số, lý thuyết số, toán ứng dụng - quy hoạch tuyến tính, lý thuyết điều khiển tối ưu. Vì vậy, chủ đề này có liên quan và kiến thức về vấn đề này rất quan trọng đối với xã hội hiện đại.

Phần chính

Khối đa diện là một khối có bề mặt bao gồm một số hữu hạn các đa giác.

Chúng ta hãy đưa ra một định nghĩa về khối đa diện tương đương với định nghĩa đầu tiên về khối đa diện.

đa diện – Đây là hình là hợp của một số hữu hạn các tứ diện thỏa mãn các điều kiện sau:

1) hai tứ diện không có điểm chung, hoặc có một đỉnh chung, hoặc chỉ có một cạnh chung, hoặc toàn bộ một mặt chung;

2) từ mỗi khối tứ diện này đến khối tứ diện khác, bạn có thể đi dọc theo một chuỗi các khối tứ diện, trong đó mỗi khối tứ diện tiếp theo liền kề với khối trước đó dọc theo toàn bộ một mặt.

phần tử đa diện

Mặt của khối đa diện là một đa giác nhất định (đa giác là một vùng kín giới hạn có ranh giới bao gồm một số hữu hạn các đoạn).

Các cạnh của các mặt được gọi là các cạnh của khối đa diện và các đỉnh của các mặt được gọi là các đỉnh của khối đa diện. Các phần tử của một khối đa diện, ngoài các đỉnh, các cạnh và các mặt của nó, còn bao gồm các góc phẳng của các mặt và các góc nhị diện ở các cạnh của nó. Góc nhị diện ở một cạnh của khối đa diện được xác định bởi các mặt của nó tiến gần đến cạnh này.

Phân loại khối đa diện

đa diện lồi - là một khối đa diện, hai điểm bất kỳ của chúng có thể nối với nhau bằng một đoạn thẳng. Khối đa diện lồi có nhiều tính chất đáng chú ý.

Định lý Euler.Đối với mọi khối đa diện lồi V-R+G=2,

Ở đâu TRONG – số đỉnh của nó, R - số lượng xương sườn của nó, G - số mặt của nó.

Định lý Cauchy. Hai khối đa diện lồi khép kín, gồm các mặt tương ứng bằng nhau, thì bằng nhau.

Một khối đa diện lồi được coi là đều nếu tất cả các mặt của nó đều là các đa giác đều bằng nhau và có cùng số cạnh hội tụ tại mỗi đỉnh của nó.

đa diện đều

Một khối đa diện được gọi là đều nếu, thứ nhất, nó lồi, thứ hai, tất cả các mặt của nó đều là các đa giác đều bằng nhau, thứ ba, cùng số mặt gặp nhau tại mỗi đỉnh của nó, và thứ tư, tất cả các góc nhị diện của nó đều bằng nhau.

Có năm khối đa diện đều lồi - khối tứ diện, khối tám mặt và khối hai mươi mặt có mặt hình tam giác, khối lập phương (hình lục giác) có mặt vuông và khối mười hai mặt có mặt ngũ giác. Bằng chứng về sự thật này đã được biết đến từ hơn hai nghìn năm nay; với bằng chứng này và nghiên cứu về năm vật thể đều đặn, Các yếu tố của Euclid (nhà toán học Hy Lạp cổ đại, tác giả của các chuyên luận lý thuyết đầu tiên về toán học đã đến với chúng ta) đã được hoàn thành. Tại sao các khối đa diện thông thường lại có được những cái tên như vậy? Điều này là do số lượng khuôn mặt của họ. Một khối tứ diện có 4 mặt, được dịch từ tiếng Hy Lạp “tetra” - bốn, “hedron” - mặt. Một khối lục giác (khối lập phương) có 6 mặt, một “hexa” có sáu mặt; bát diện - bát diện, "octo" - tám; khối mười hai mặt - khối mười hai mặt, "dodeca" - mười hai; Khối 20 mặt có 20 mặt và icosi có 20 mặt.

2.3. Các loại khối đa diện đều:

1) Tứ diện đều(gồm bốn tam giác đều. Mỗi đỉnh là đỉnh của ba tam giác. Do đó tổng các góc phẳng tại mỗi đỉnh là 180 0);

2)khối lập phương- một hình bình hành, tất cả các mặt đều là hình vuông. Khối lập phương được tạo thành từ sáu hình vuông. Mỗi đỉnh của hình lập phương là đỉnh của ba hình vuông. Do đó, tổng các góc phẳng ở mỗi đỉnh là 270 0.

3) bát diện đều hoặc đơn giản bát diện– một khối đa diện có tám mặt tam giác đều và bốn mặt gặp nhau ở mỗi đỉnh. Hình bát diện được tạo thành từ tám hình tam giác đều. Mỗi đỉnh của hình bát diện đều là đỉnh của bốn hình tam giác. Do đó, tổng các góc phẳng ở mỗi đỉnh là 240 0. Nó có thể được xây dựng bằng cách gấp các đáy của hai kim tự tháp, đáy của chúng là hình vuông và các mặt bên là hình tam giác đều. Các cạnh của một hình bát diện có thể thu được bằng cách nối tâm của các mặt liền kề của hình lập phương, nhưng nếu chúng ta nối tâm của các mặt liền kề của một hình bát diện đều, chúng ta sẽ có được các cạnh của hình lập phương. Người ta nói rằng hình lập phương và hình bát diện là đối ngẫu của nhau.

4)icosahedron- gồm hai mươi hình tam giác đều. Mỗi đỉnh của khối hai mươi mặt đều là đỉnh của năm hình tam giác. Do đó, tổng các góc phẳng ở mỗi đỉnh bằng 300 0.

5) khối mười hai mặt- một khối đa diện được tạo thành từ mười hai hình ngũ giác đều. Mỗi đỉnh của khối mười hai mặt là đỉnh của ba hình ngũ giác đều. Do đó, tổng các góc phẳng ở mỗi đỉnh là 324 0.

Khối mười hai mặt và khối hai mươi mặt cũng đối lập với nhau theo nghĩa là bằng cách nối tâm của các mặt liền kề của khối mười hai mặt với các đoạn, chúng ta sẽ có được một khối mười hai mặt và ngược lại.

Một tứ diện đều có tính chất đối ngẫu với chính nó.

Hơn nữa, không có khối đa diện đều nào có các mặt là lục giác, bảy giác đều và n-giác nói chung với n ≥ 6.

Một khối đa diện đều là một khối đa diện trong đó tất cả các mặt đều là các đa giác đều bằng nhau và tất cả các góc nhị diện đều bằng nhau. Nhưng cũng có những khối đa diện trong đó tất cả các góc đa diện đều bằng nhau và các mặt đều là các đa giác đều nhưng đối diện nhau. Các khối đa diện loại này được gọi là khối đa diện bán đều đều. Khối đa diện thuộc loại này lần đầu tiên được phát hiện bởi Archimedes. Ông đã mô tả chi tiết 13 khối đa diện, sau này được đặt tên là thi thể của Archimedes để vinh danh nhà khoa học vĩ đại. Đó là khối tứ diện cụt, khối thập diện cụt, khối hai mươi mặt cụt, khối lập phương cụt, khối mười hai mặt cụt, khối bốn mặt, khối mười hai mặt, khối ba mặt cụt, khối mười hai mặt cụt, khối mười hai mặt hình thoi, khối mười hai mặt hình thoi, khối lập phương mũi hếch, khối lập phương mũi hếch) khối mười hai mặt.

2.4. Khối đa diện bán đều hoặc khối Archimedean là khối đa diện lồi có hai tính chất:

1. Tất cả các mặt đều là đa giác đều có từ hai loại trở lên (nếu tất cả các mặt đều là đa giác đều cùng loại thì là khối đa diện đều).

2. Đối với bất kỳ cặp đỉnh nào cũng có sự đối xứng của khối đa diện (tức là chuyển động biến khối đa diện đó thành chính nó) truyền từ đỉnh này sang đỉnh kia. Đặc biệt, tất cả các góc ở đỉnh đa diện đều bằng nhau.

Ngoài các khối đa diện bán đều, từ các khối đa diện đều - chất rắn Platonic - người ta có thể thu được cái gọi là khối đa diện hình sao đều. Chỉ có bốn trong số chúng, chúng còn được gọi là vật thể Kepler-Poinsot. Kepler đã phát hiện ra một khối mười hai mặt nhỏ mà ông gọi là gai hay con nhím, và một khối mười hai mặt lớn. Poinsot đã phát hiện ra hai khối đa diện hình sao đều khác, tương ứng là kép với khối đa diện đầu tiên hai: khối mười hai mặt hình sao lớn và khối hai mươi mặt lớn.

Hai tứ diện đi qua nhau tạo thành một bát diện. Johannes Kepler đặt cho hình này cái tên “stella octangula” - “ngôi sao bát giác”. Nó cũng được tìm thấy trong tự nhiên: đây được gọi là tinh thể kép.

Trong định nghĩa về một khối đa diện đều, từ “lồi” không được nhấn mạnh một cách có chủ ý - dựa trên sự hiển nhiên rõ ràng. Và nó có nghĩa là một yêu cầu bổ sung: "và tất cả các mặt của chúng nằm trên một mặt của mặt phẳng đi qua bất kỳ mặt nào trong số chúng." Nếu chúng ta từ bỏ hạn chế như vậy, thì đối với các khối Platonic, ngoài “hình bát diện mở rộng”, chúng ta sẽ phải thêm bốn khối đa diện nữa (chúng được gọi là khối Kepler-Poinsot), mỗi khối sẽ “gần như đều đặn”. Tất cả đều có được nhờ sự “đóng vai chính” của Platonov nghĩa là bằng cách kéo dài các cạnh của nó cho đến khi chúng giao nhau với nhau, và do đó được gọi là hình sao. Khối lập phương và khối tứ diện không tạo ra các hình mới - các mặt của chúng, cho dù bạn có tiếp tục thế nào đi chăng nữa, cũng không giao nhau.

Nếu bạn kéo dài tất cả các mặt của hình bát diện cho đến khi chúng giao nhau, bạn sẽ có được một hình xuất hiện khi hai khối tứ diện xuyên qua - "hình bát giác", được gọi là "mở rộng". bát diện."

Khối hai mươi mặt và khối mười hai mặt cung cấp cho thế giới bốn khối "khối đa diện gần như đều đặn" cùng một lúc. Một trong số đó là khối mười hai mặt hình sao nhỏ, được Johannes Kepler thu được lần đầu tiên.

Trong nhiều thế kỷ, các nhà toán học đã không công nhận quyền được gọi là đa giác của tất cả các loại sao do các cạnh của chúng giao nhau. Tuy nhiên, Ludwig Schläfli không loại một vật thể hình học ra khỏi họ khối đa diện chỉ vì các mặt của nó giao nhau; tuy nhiên, ông vẫn kiên quyết ngay khi cuộc trò chuyện chuyển sang khối mười hai mặt hình sao nhỏ. Lập luận của ông rất đơn giản và có sức thuyết phục: con vật Kepler này không tuân theo công thức Euler! Các gai của nó được hình thành mười hai mặt, ba mươi cạnh và mười hai đỉnh, và do đó, B+G-R hoàn toàn không bằng hai.

Schläfli vừa đúng vừa sai. Tất nhiên, con nhím hình học không gai góc đến mức chống lại công thức không thể sai lầm. Bạn chỉ cần không coi nó được hình thành bởi 12 mặt hình ngôi sao giao nhau mà hãy nhìn nó như một khối hình học đơn giản, trung thực được tạo thành từ 60 hình tam giác, có 90 cạnh và 32 đỉnh.

Khi đó, B+G-R=32+60-90, như mong đợi, bằng 2. Nhưng khi đó, từ “đúng” không áp dụng cho khối đa diện này - xét cho cùng, các mặt của nó bây giờ không phải là các cạnh đều mà chỉ là các tam giác cân. Kepler đã không nhận ra rằng con số mình nhận được có gấp đôi.

Khối đa diện, còn được gọi là “khối mười hai mặt lớn”, được xây dựng bởi nhà hình học người Pháp Louis Poinsot hai trăm năm sau các hình vẽ ngôi sao của Kepler.

Khối hai mươi mặt lớn được mô tả lần đầu tiên bởi Louis Poinsot vào năm 1809. Và một lần nữa Kepler, sau khi nhìn thấy một khối mười hai mặt lớn có hình sao, đã để lại vinh dự khám phá ra hình tượng thứ hai cho Louis Poinsot. Những số liệu này cũng tuân theo một nửa công thức Euler.

Công dụng thực tế

Khối đa diện trong tự nhiên

Các khối đa diện đều là những hình dạng có lợi nhất, đó là lý do tại sao chúng phổ biến trong tự nhiên. Điều này được xác nhận bởi hình dạng của một số tinh thể. Ví dụ, tinh thể muối ăn có hình khối. Trong sản xuất nhôm, thạch anh nhôm-kali được sử dụng, tinh thể đơn có hình dạng bát diện đều. Việc sản xuất axit sulfuric, sắt và các loại xi măng đặc biệt không thể thực hiện được nếu không có pyrit lưu huỳnh. Các tinh thể của hóa chất này có hình khối mười hai mặt. Antimon natri sunfat, một chất được các nhà khoa học tổng hợp, được sử dụng trong nhiều phản ứng hóa học khác nhau. Tinh thể natri antimon sunfat có hình dạng tứ diện. Khối đa diện đều cuối cùng, khối 20 mặt đều có hình dạng của tinh thể boron.

Các khối đa diện hình ngôi sao có tính trang trí rất cao, cho phép chúng được sử dụng rộng rãi trong ngành trang sức để sản xuất các loại trang sức. Chúng cũng được sử dụng trong kiến trúc. Nhiều dạng khối đa diện hình sao được tự nhiên gợi ý. Bông tuyết là khối đa diện hình ngôi sao. Từ xa xưa, con người đã cố gắng mô tả tất cả các loại bông tuyết có thể có và biên soạn các tập bản đồ đặc biệt. Hàng ngàn loại bông tuyết khác nhau hiện đã được biết đến.

Các khối đa diện đều cũng được tìm thấy trong tự nhiên sống. Ví dụ, bộ xương của sinh vật đơn bào Feodaria (Circjgjnia icosahtdra) có hình dạng giống như một khối hai mươi mặt. Hầu hết các loài feodaria sống ở độ sâu của biển và làm mồi cho cá san hô. Nhưng loài động vật đơn giản nhất tự bảo vệ mình bằng 12 chiếc gai mọc ra từ 12 đỉnh của bộ xương. Nó trông giống một khối đa diện hình sao hơn.

Chúng ta cũng có thể quan sát khối đa diện ở dạng hoa. Một ví dụ nổi bật là xương rồng.

Thông tin liên quan.

Khối đa diện không chỉ chiếm một vị trí nổi bật trong hình học mà còn được tìm thấy trong đời sống hằng ngày của mỗi người. Chưa kể những đồ gia dụng được tạo ra nhân tạo dưới dạng đa giác khác nhau, từ hộp diêm đến các yếu tố kiến trúc, trong tự nhiên còn có những tinh thể ở dạng khối lập phương (muối), lăng kính (pha lê), kim tự tháp (scheelite), bát diện (kim cương). ), v.v. d.

Khái niệm khối đa diện, các loại khối đa diện trong hình học

Hình học như một môn khoa học bao gồm phép đo lập thể mặt cắt, nghiên cứu các đặc điểm và tính chất của các khối thể tích, các cạnh của chúng trong không gian ba chiều được hình thành bởi các mặt phẳng (mặt) giới hạn, được gọi là “khối đa diện”. Có hàng chục loại khối đa diện, khác nhau về số lượng và hình dạng các mặt.

Tuy nhiên, tất cả các khối đa diện đều có những đặc tính chung:

Tất cả đều có 3 thành phần không thể thiếu: một mặt (bề mặt của đa giác), một đỉnh (các góc tạo thành tại điểm giao nhau của các mặt), một cạnh (cạnh của hình hoặc đoạn tạo thành tại điểm giao nhau của hai mặt). ).
Mỗi cạnh của đa giác kết nối hai và chỉ hai mặt liền kề nhau.
Tính lồi có nghĩa là vật chỉ nằm hoàn toàn trên một phía của mặt phẳng chứa một trong các mặt. Quy tắc áp dụng cho tất cả các mặt của khối đa diện. Trong phép đo lập thể, những hình hình học như vậy được gọi là khối đa diện lồi. Ngoại lệ là các khối đa diện hình sao, là dẫn xuất của các khối hình học đa diện đều.

Khối đa diện có thể được chia thành:

Các loại khối đa diện lồi, gồm các lớp sau: thường hoặc cổ điển (lăng kính, hình chóp, hình bình hành), đều (còn gọi là khối Platonic), bán đều (tên gọi khác là khối Archimedean).
Khối đa diện không lồi (hình sao).

Lăng kính và tính chất của nó

Lập thể như một nhánh của hình học nghiên cứu các tính chất của hình ba chiều, các loại khối đa diện (lăng kính trong số đó). Lăng kính là một vật thể hình học nhất thiết phải có hai mặt hoàn toàn giống nhau (chúng còn được gọi là đáy) nằm trong các mặt phẳng song song và số cạnh thứ n là hình bình hành. Ngược lại, lăng kính cũng có một số loại, bao gồm các loại khối đa diện như:

Một hình bình hành được hình thành nếu đáy là hình bình hành - một đa giác có 2 cặp góc đối diện bằng nhau và hai cặp cạnh đối diện bằng nhau.
có các gân vuông góc với đáy.
được đặc trưng bởi sự hiện diện của các góc gián tiếp (trừ 90) giữa các cạnh và đế.
Một lăng kính đều được đặc trưng bởi các đáy có dạng các mặt bên bằng nhau.

Tính chất cơ bản của lăng kính:

Các căn cứ đồng dạng.
Tất cả các cạnh của lăng kính đều bằng nhau và song song với nhau.
Tất cả các mặt bên đều có dạng hình bình hành.

Kim tự tháp

Kim tự tháp là một khối hình học bao gồm một đáy và số lượng các mặt tam giác thứ n nối với nhau tại một điểm - đỉnh. Cần lưu ý rằng nếu các mặt bên của kim tự tháp nhất thiết phải được biểu thị bằng hình tam giác, thì ở đáy có thể có một đa giác tam giác, một hình tứ giác, một hình ngũ giác, v.v. Trong trường hợp này, tên của kim tự tháp sẽ tương ứng với đa giác ở đáy. Ví dụ: nếu ở đáy của một kim tự tháp có một hình tam giác - đây là hình tứ giác, v.v.

Kim tự tháp là khối đa diện hình nón. Các loại khối đa diện trong nhóm này, ngoài những loại được liệt kê ở trên, còn bao gồm các đại diện sau:

có một đa giác đều ở đáy và chiều cao của nó được chiếu vào tâm của một vòng tròn nội tiếp ở đáy hoặc được bao quanh nó.
Một hình chóp hình chữ nhật được hình thành khi một trong các cạnh bên cắt đáy theo một góc vuông. Trong trường hợp này, cạnh này cũng có thể được gọi là chiều cao của kim tự tháp.

Tính chất của kim tự tháp:

Nếu tất cả các cạnh bên của hình chóp bằng nhau (có cùng chiều cao) thì chúng đều cắt với đáy một góc và xung quanh đáy bạn có thể vẽ một đường tròn có tâm trùng với hình chiếu của đỉnh của hình chóp. kim tự tháp.
Nếu một đa giác đều nằm ở đáy của hình chóp thì tất cả các cạnh bên đều bằng nhau và các mặt là hình tam giác cân.

Khối đa diện đều: loại và tính chất của khối đa diện

Trong phép đo lập thể, một vị trí đặc biệt được chiếm bởi các khối hình học có các mặt hoàn toàn bằng nhau, tại các đỉnh của chúng có cùng số cạnh được nối với nhau. Những vật thể này được gọi là khối Platonic, hay khối đa diện đều. Chỉ có năm loại khối đa diện có các đặc tính sau:

Tứ diện.
Lục giác.
Bát diện.
Khối mười hai mặt.
Icosahedron.

Các khối đa diện thông thường có tên theo nhà triết học Hy Lạp cổ đại Plato, người đã mô tả các khối hình học này trong các tác phẩm của mình và liên kết chúng với các yếu tố tự nhiên: đất, nước, lửa, không khí. Hình thứ năm được cho là có sự tương đồng với cấu trúc của Vũ trụ. Theo ông, nguyên tử của các nguyên tố tự nhiên có hình dạng giống như các khối đa diện đều. Nhờ đặc tính hấp dẫn nhất của chúng - tính đối xứng, những vật thể hình học này không chỉ được các nhà toán học và triết học cổ đại mà còn cả các kiến trúc sư, nghệ sĩ và nhà điêu khắc ở mọi thời đại quan tâm. Sự hiện diện của chỉ 5 loại khối đa diện có tính đối xứng tuyệt đối được coi là một phát hiện cơ bản, thậm chí chúng còn gắn liền với nguyên lý thần thánh.

Hexahedron và tính chất của nó

Ở dạng hình lục giác, những người kế vị Plato cho rằng có sự tương đồng với cấu trúc của các nguyên tử trên trái đất. Tất nhiên, hiện tại giả thuyết này đã bị bác bỏ hoàn toàn, tuy nhiên, điều đó không ngăn cản những nhân vật ở thời hiện đại thu hút tâm trí của những nhân vật nổi tiếng bằng tính thẩm mỹ của họ.

Trong hình học, một khối lục giác, còn được gọi là khối lập phương, được coi là trường hợp đặc biệt của một hình bình hành, do đó, nó là một loại lăng kính. Theo đó, các tính chất của hình lập phương có liên quan đến điểm khác biệt duy nhất là tất cả các mặt và các góc của hình lập phương đều bằng nhau. Các thuộc tính sau đây theo sau:

Tất cả các cạnh của hình lập phương đều bằng nhau và nằm trong các mặt phẳng song song với nhau.
Tất cả các mặt đều là hình vuông bằng nhau (có 6 mặt trong hình lập phương), bất kỳ mặt nào trong số đó có thể được lấy làm cơ sở.
Tất cả các góc liên diện đều bằng 90.
Mỗi đỉnh có số cạnh bằng nhau, tức là 3.
Hình lập phương có 9, tất cả đều cắt nhau tại giao điểm của các đường chéo của khối lục giác, gọi là tâm đối xứng.

tứ diện

Tứ diện là một tứ diện có các mặt bằng nhau có dạng hình tam giác, mỗi đỉnh là điểm nối của ba mặt.

Tính chất của tứ diện đều:

Tất cả các mặt của tứ diện - điều này có nghĩa là tất cả các mặt của tứ diện đều bằng nhau.
Vì đáy được biểu diễn bằng một hình hình học đều, nghĩa là nó có các cạnh bằng nhau nên các mặt của tứ diện đều hội tụ một góc, nghĩa là tất cả các góc đều bằng nhau.
Tổng các góc phẳng ở mỗi đỉnh là 180, vì tất cả các góc đều bằng nhau nên mọi góc của tứ diện đều là 60.
Mỗi đỉnh được chiếu tới điểm giao nhau của các độ cao của mặt đối diện (trực tâm).

Bát diện và tính chất của nó

Khi mô tả các loại khối đa diện đều, người ta không thể không chú ý đến một vật thể như khối bát diện, có thể được biểu diễn trực quan dưới dạng hai hình chóp đều hình tứ giác được dán lại với nhau ở đáy.

Tính chất của bát diện:

Chính cái tên của một khối hình học đã gợi ý số lượng mặt của nó. Hình bát diện bao gồm 8 hình tam giác đều bằng nhau, tại mỗi đỉnh có số mặt bằng nhau hội tụ, cụ thể là 4.
Vì tất cả các mặt của hình bát diện đều bằng nhau nên các góc phân cách của nó cũng bằng nhau, mỗi góc bằng 60 và tổng các góc phẳng của bất kỳ đỉnh nào là 240.

khối mười hai mặt

Nếu chúng ta tưởng tượng rằng tất cả các mặt của một khối hình học là một hình ngũ giác đều, thì chúng ta sẽ có một khối mười hai mặt - một hình gồm 12 đa giác.

Tính chất của khối mười hai mặt:

Ba mặt cắt nhau ở mỗi đỉnh.
Tất cả các mặt đều bằng nhau và có cùng độ dài cạnh cũng như diện tích bằng nhau.
Khối mười hai mặt có 15 trục và mặt phẳng đối xứng, và bất kỳ trục nào trong số chúng đều đi qua đỉnh của mặt và điểm giữa của cạnh đối diện với nó.

icosahedron

Không kém phần thú vị so với khối mười hai mặt, hình khối hai mươi mặt là một khối hình học ba chiều với 20 mặt bằng nhau. Trong số các thuộc tính của khối 20 mặt thông thường, có thể lưu ý những điều sau:

Tất cả các mặt của khối 20 mặt đều là hình tam giác cân.
Năm mặt gặp nhau ở mỗi đỉnh của khối đa diện và tổng các góc kề nhau của đỉnh là 300.
Khối hai mươi mặt, giống như khối mười hai mặt, có 15 trục và mặt phẳng đối xứng đi qua trung điểm của các mặt đối diện.

Đa giác bán đều

Ngoài các khối Platonic, nhóm các khối đa diện lồi còn bao gồm các khối Archimedean, là các khối đa diện đều bị cắt cụt. Các loại khối đa diện trong nhóm này có các tính chất sau:

Các vật thể hình học có một số loại mặt bằng nhau theo từng cặp, ví dụ, một tứ diện cụt có 8 mặt, giống như một tứ diện đều, nhưng trong trường hợp vật thể Archimedean, 4 mặt sẽ là hình tam giác và 4 mặt sẽ là hình lục giác.
Mọi góc của một đỉnh đều bằng nhau.

khối đa diện sao

Đại diện của các dạng hình học không thể tích là các khối đa diện hình sao, các mặt của chúng giao nhau. Chúng có thể được hình thành bằng sự hợp nhất của hai vật thể ba chiều thông thường hoặc là kết quả của sự mở rộng khuôn mặt của chúng.

Vì vậy, các khối đa diện hình sao như vậy được gọi là: các dạng hình sao của bát diện, khối mười hai mặt, khối hai mươi mặt, khối bốn mặt, khối mười hai mặt.